【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为A、B、C、D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表：
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
（1）表中的a=________，b=________；
（2）根据表中数据，求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；
（3）若该校有学生1000名，根据调查结果估计该校学生中类别为C的人数约为多少？
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件，已知生产一件A种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B种产品用甲种原料4千克，乙种原料10千克，可获利1200元．
（1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；
（2）设生产A、B两种产品总利润为y元，其中一种产品生产件数为x件，试写出y与x之间的函数关系式，并利用函数的性质说明那种方案获利最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（ ）
A. （3，-1） B. （-1，-1） C. （1，1） D. （-2，-1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一只不透明的袋子中装有红球2个和白球2个，这些球除颜色外其余都相同，小明从袋子中任意摸出一球，记下颜色后不放回，若小明再从剩余的球中任取一球，请你用列表法或树状图的方法，求小明两次都摸出红球的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，AB=BD，点E、F分别在BC、CD上，且BE=CF，连接BF、DE交于点M，延长ED到H使DH=BM，连接AM，AH，则以下四个结论：
①△BDF≌△DCE；②∠BMD=120°；③△AMH是等边三角形；④S四边形ABCD= 
AM2．
其中正确结论的个数是（ ）
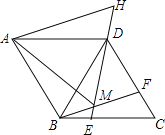
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABO中，AB⊥OB，OB=
，AB=1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1的坐标为
A．（﹣1，
） B．（﹣1，）或（﹣2，0） C．（，﹣1）或（0，﹣2） D．（，﹣1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（ ）
A．①③ B．②③ C．②④ D．②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】目前节能灯在城市已基本普及，为响应号召，某商场计划购进甲，乙两种节能灯共200只，这两种节能灯的进价、售价如下表：
进价（元/只） | 售价（元/只） | |
甲型 | 20 | 30 |
乙型 | 30 | 45 |
（1）若购进甲，乙两种节能灯共用去5200元，求甲、乙两种节能灯各进多少只？
（2）若商场准备用不多于5400元购进这两种节能灯，问甲型号的节能灯至少进多少只？
（3）在（2）的条件下，该商场销售完200只节能灯后能否实现盈利超过2690元的目标？若能请你给出相应的采购方案；若不能说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）先化简，再求值：3x2﹣（2x2﹣xy+y2）+（﹣x2+3xy+2y2），其中x=﹣2，y=3．
（2）一个角比它的余角大20°，求这个角的补角度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
