
分析 先根据ASA判定△DCE≌△DFB,得出DE=DF,再根据∠EDF=90°,得到△DEF是等腰直角三角形,进而得出∠FEG=45°,再分三种情况进行讨论:当G在线段CB延长线上时;当G与B重合时;当G在线段BC上时,分别求得FG的长即可.
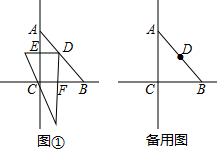
解答 解:∵AC=BC,∠C=90°,D为AB中点,连接CD,
∴CD平分∠ACB,CD⊥AB,
∵∠DCB=∠B=45°,
∴CD=DB,
∵∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
在△DCE和△DFB中,
$\left\{\begin{array}{l}{∠EDC=∠FDB}\\{CD=DB}\\{∠DCE=∠B}\end{array}\right.$,
∴△DCE≌△DFB(ASA),
∴DE=DF,
又∵∠EDF=90°,
∴△DEF是等腰直角三角形,
∴∠FEG=45°,
如图,当G在线段CB延长线上时,∠FGE<45°,∠EFG>90°,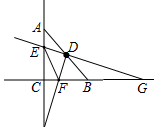
∴EF<GF,
∴△EFG不是等腰三角形;
如图,当G与B重合时,E与A重合,F与C重合,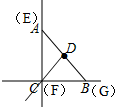
此时FE=AC=2,FG=CB=2,
如图,当G在线段BC上时,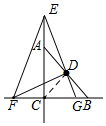
根据∠EGF>45°,∠EFG>45°,∠FEG=45°,可得EF=EG,
∵EC⊥FG,
∴FC=CG,
∵∠EDF=90°,
∴∠FDG=90°,
∴DC=$\frac{1}{2}$FG,即FG=2CD,
又∵等腰Rt△ABC中,CD=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$,
∴FG=2$\sqrt{2}$.
综上所述,当△EFG为等腰三角形时,则FG=2或2$\sqrt{2}$.
故答案为:2或2$\sqrt{2}$.
点评 本题主要考查了旋转的性质,等腰直角三角形的判定以及全等三角形的判定与性质的综合应用;等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.解决问题的关键是判定△DEF是等腰直角三角形,解题时注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
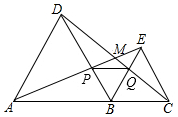 如图,点A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接AE和CD,AE分别交BD、CD于点P、M,CD交BE于点Q,连接PQ.
如图,点A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接AE和CD,AE分别交BD、CD于点P、M,CD交BE于点Q,连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以AB为直径的⊙O中,CD是弦,CD∥AB,连接AC,BD交于点M.
如图,以AB为直径的⊙O中,CD是弦,CD∥AB,连接AC,BD交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(m-x)(n-x) | B. | x2(m-x)(n-x) | C. | $\frac{1}{3}$x(m-2n)(n-2x) | D. | x(m-2x)(n-2x) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 种子个数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 发芽种子个数 | 94 | 187 | 282 | 338 | 435 | 530 | 624 | 718 | 814 | 901 |
| 发芽种子频率 | 0.940 | 0.935 | 0.940 | 0.845 | 0.870 | 0.883 | 0.891 | 0.898 | 0.904 | 0.901 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com