
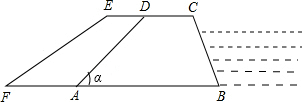
 如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.
如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度(即tanα)为1:1.2,坝高10米,为了提高坝的防洪能力,由相关部门决定加固堤坝,要求将坝顶CD加宽2米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为1000米.分析 (1)欲求完成该工程需要多少土方,根据体积公式,在本题中,必须求出四边形AFED的面积,上底、高为已知,只需用两次坡度比求出AF的长.
(2)根据题中两个等量关系列方程组解答即可.
解答 解:(1)如图所示:作DG⊥AB于G,作EH⊥AB于H,
∴EH∥DG,∠EHG=∠DGB=90°,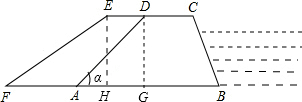
又∵CD∥AB,
∴四边形EHGD是矩形,
∴EH=DG=10米,
∵$\frac{DG}{AG}$=$\frac{1}{1.2}$,
∴AG=12米,
∵$\frac{EH}{FH}$=$\frac{1}{1.4}$,∴FH=14米,
∴FA=FH+GH-AG=14+2-12=4(米)
∴S四边形ADEF=$\frac{1}{2}$(ED+AF)•EH=$\frac{1}{2}$(4+2)×10=30(平方米)
V=30×1000=30000(立方米);
答:需要30000立方米土方.
(2)设甲队原计划每天完成x立方米土方,乙队原计划每天完成y立方米土方.
根据题意,得$\left\{\begin{array}{l}{20(x+y)=30000}\\{15[(1+30%)x+(1+40%)y]=30000}\end{array}\right.$,
解之,得,$\left\{\begin{array}{l}{x=1000}\\{y=500}\end{array}\right.$,
答:甲队原计划每天完成1000立方米土方,
乙队原计划每天完成500立方米土方.
点评 此题考查了解直角三角形的应用、二元一次方程组的应用以及梯形面积的计算,正确应用锐角三角函数关系得出AF的长是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组邻边相等 | B. | 一组对边平行 | ||
| C. | 两组对边分别相等 | D. | 两组对边的和相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
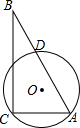 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.
如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com