
如图,AO是△ABC的中线,⊙O与AB相切于点D.

(1)要使⊙O与AC边也相切,应增加条件__ _______.
(2)增加条件后,请你证明⊙O与AC相切.
(1)AB=AC(或∠B=∠C或AO平分∠BAC或AO⊥BC);(2)证明见试题解析.
【解析】
试题分析:(1)要使⊙O与AC边也相切,则应满足AO⊥BC,结合已知OB=OC,所以只要符合等腰三角形的三线合一即可;
(2)根据所添加的条件,利用等腰三角形的三线合一即可证明.
试题解析:(1)解:AB=AC(或∠B=∠C或AO平分∠BAC或AO⊥BC).
(2)证明:过O作OE⊥AC于E,连OD;∵AB切⊙O于D,∴OD⊥AB.∵AB=AC,AO是BC边上中线,∴OA平分∠BAC,又∵OD⊥AB于D,OE⊥AC于E,∴OE=OD,∴AC是⊙O的切线.
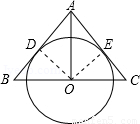
考点:1.切线的判定;2.等腰三角形的性质.


科目:初中数学 来源: 题型:
 20、如图,AO是△ABC的中线,⊙O与AB边相切于点D.
20、如图,AO是△ABC的中线,⊙O与AB边相切于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AO是△ABC的中线,⊙O与AB边相切于点D.
如图,AO是△ABC的中线,⊙O与AB边相切于点D.查看答案和解析>>
科目:初中数学 来源:2007-2008学年九年级(上)期中数学试卷(解析版) 题型:解答题
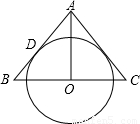
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(16)(解析版) 题型:解答题
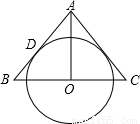
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com