
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

科目:初中数学 来源: 题型:
【题目】为了了解全年级学生英语作业的完成情况,帮助英语学习成绩差的学生尽快提高成绩,班主任和英语教师从全年级![]() 名学生中抽取
名学生中抽取![]() 名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占
名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占![]() ,明显高于他平时观察到的比例,请回答下列问题:
,明显高于他平时观察到的比例,请回答下列问题:
(1)英语教师所用的调查方式是_______;
(2)如果老师的英语作业检查只得“差”的同学有![]() 名,那么估计全年级的英语作业中可能有多少同学得“差”;
名,那么估计全年级的英语作业中可能有多少同学得“差”;
(3)通过问卷调查,老师得到的数据与事实不符,请你解释这个统计数字失真的原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设①踢毽子;②篮球;③跳绳;④乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下不完整的两个统计图,依据图中信息,得出下列结论中正确的是( )
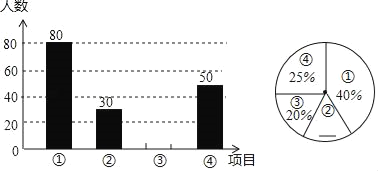
A. 本次共调查300名学生
B. 扇形统计图中,喜欢篮球项目的学生部分所对应的扇形圆心角大小为45°
C. 喜欢跳绳项日的学生人数为60人
D. 喜欢篮球项目的学生人数为30人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】果园要将批水果运往某地,打算租用某汽车运输公司的甲、乙两种货车.以前两次租用这两种货车的信息如表所示:
第一次 | 第二次 | |
甲种货车车辆数(辆) |
|
|
乙种货车车辆数(辆) |
|
|
累计货运量(吨) |
|
|
(1)甲、乙两种货车每辆每次可分别运水果多少吨?
(2)果园现从该汽车运输公司租用甲、乙两种货车共![]() 辆,要求一次运 送这批水果不少于
辆,要求一次运 送这批水果不少于![]() 吨.请你通过计算,求出果园这次至少租用甲种货车多少辆?
吨.请你通过计算,求出果园这次至少租用甲种货车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相较于点O,EF过点O,且与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长是( )

A.16B.14C.12D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
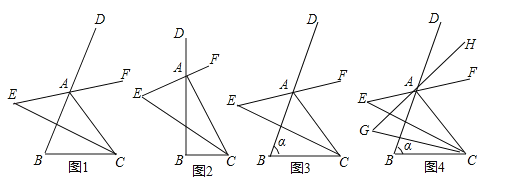
【题目】如图,在△ABC中,分别作其内角∠ACB与外角∠DAC的角平分线,且两条角平分线所在的直线交于点E
(1)填空:①如图1,若∠B=60°,则∠E= ;
②如图2,若∠B=90°,则∠E= ;
(2)如图3,若∠B=α,求∠E的度数;
(3)如图4,仿照(2)中的方法,在(2)的条件下分别作∠EAB与∠ECB的角平分线,且两条角平分线交于点G,求∠G的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B坐标为(-2,1).
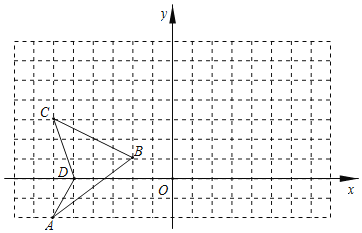
(1)请在图中画出将四边形ABCD关于y轴对称后的四边形A′B′C′D′,并直接写出点A′、B′、C′、D′的坐标;
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】龙人文教用品商店欲购进![]() 、
、![]() 两种笔记本,用160元购进的
两种笔记本,用160元购进的![]() 种笔记本与用240元购进的
种笔记本与用240元购进的![]() 种笔记本数量相同,每本
种笔记本数量相同,每本![]() 种笔记本的进价比每本
种笔记本的进价比每本![]() 种笔记本的进价贵10元.
种笔记本的进价贵10元.
(1)求![]() 、
、![]() 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?
(2)若该商店准备购进![]() 、
、![]() 两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进
两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进![]() 种笔记本多少本?
种笔记本多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com