
【题目】如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先测量出窗口A到地面的距离AB=16m,又测得从A处看建筑物底部C的俯角为![]() =30°,看建筑物顶部D的仰角为
=30°,看建筑物顶部D的仰角为![]() =45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.
=45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.
(1)求AB与CD之间的距离(结果保留根号);
(2)求建筑物CD的高度(结果精确到0.1m).(参考数据:![]() ,
,![]() )
)

科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
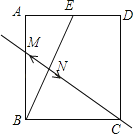
【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于![]() 的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
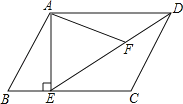
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3![]() ,AE=3,求AF的长;
,AE=3,求AF的长;
(3)若CD=CE,则直线CD是以点E为圆心,AE长为半径的圆的切线.试证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市从不同学校随机抽取100名初中生对“使用数学教辅用书的册数”进行调查,统计结果如下:
册数 | 0 | 1 | 2 | 3 |
人数 | 10 | 20 | 30 | 40 |
关于这组数据,下列说法正确的是( )
A.众数是2册B.中位数是2册
C.平均数是3册D.方差是1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
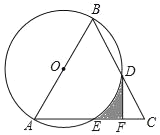
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC,AC于点D,E,过点D作DF⊥AC于点F
(1)求证:DF是⊙O的切线;
(2)若∠C=60°,⊙O的半径为2,求由弧DE,线段DF,EF围成的阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会大课堂的数学实践活动中,王老师要求同学们测量教室窗户边框上的点C到地面的距离即CD的长,小英测量的步骤及测量的数据如下:
(1)在地面上选定点A, B,使点A,B,D在同一条直线上,测量出![]() 、
、![]() 两点间的距离为9米;
两点间的距离为9米;
(2)在教室窗户边框上的点C点处,分别测得点![]() ,
, ![]() 的俯角∠ECA=35°,∠ECB=45°.请你根据以上数据计算出
的俯角∠ECA=35°,∠ECB=45°.请你根据以上数据计算出![]() 的长.
的长.
(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70)

查看答案和解析>>
科目:初中数学 来源: 题型:
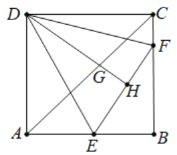
【题目】如图,正方形ABCD的边长为4,将△ADE和△CDF分别沿直线DE和DF折叠后,点A和点C同时落在点H处,且E是AB中点,射线DH交AC于G,交CB于M,则GH的长是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com