
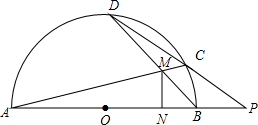
 如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.
如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB. 分析 连接OD,OC,ND,NC,DA由ON•OP=OB2,易证△ODN∽△OPD,利用对应角相等可得O,D,C,N四点共圆;由BD平分角∠CDN及M为△DCN的内心,得出M,N,A,D四点共圆,再由AB为半圆O的直径,得出∠ADB=90°,从而得出∠MNA=∠ADM=90°,即可得出MN⊥AB.
解答 证明:如图,连接OD,OC,ND,NC,DA
∵OB2=ON•OP=OD2
∴$\frac{ON}{OD}$=$\frac{OD}{OP}$,
∵∠DON=∠POD,
∴△ODN∽△OPD
∴∠DNO=∠ODC=∠OCD
∴O,D,C,N四点共圆;
∴∠CDN=∠CON=2∠CAB=2∠CDB
∴BD平分角∠CDN
又∵∠DCN=∠DOA=2∠DBA=2∠DCA
∴AC平分角∠DCN
∴M为△DCN的内心
∴$∠MND=\frac{1}{2}∠DNC=\frac{1}{2}∠DOC=∠DAC$
∴M,N,A,D四点共圆
∵AB为半圆O的直径,
∴∠ADB=90°,
∴∠MNA=∠ADM=90°,
∴MN⊥AB.
点评 本题主要考查了四点共圆,涉及三角形相似的判定与性质,角平分线,四点共圆的判定及三角形内心,解题的关键是正确作出辅助线,得出O,D,C,N四点共圆.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.
如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )| A. | 5:3 | B. | 11:7 | C. | 23:15 | D. | 47:29 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com