
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
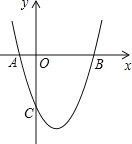
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
【答案】(1)y=x2﹣2x﹣3.(2)抛物线的对称轴x=1,顶点坐标(1,﹣4).(3)点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.
【解析】
试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得P点的坐标.
解:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴![]() AB|yP|=8,
AB|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2![]() ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图1,MN∥EF,C为两直线之间一点.
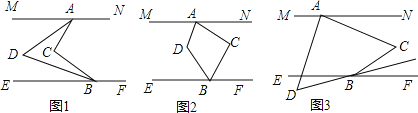
(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.
(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.
(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体内某种细胞的形状可近似看做球状,它的直径是0.00000156m,这个数据用科学记数法可表示为( )
A. 1.56×10﹣6m B. 1.56×10﹣5m C. 156×10﹣5m D. 1.56×106m
查看答案和解析>>
科目:初中数学 来源: 题型:
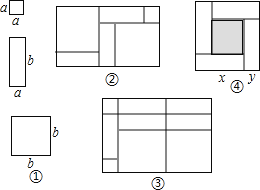
【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的 块, 块, 块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:
(1)![]() (2)x+y=m(3)x2﹣y2=mn(4)
(2)x+y=m(3)x2﹣y2=mn(4)![]()
其中正确的有
A.1个 B.2个 C.3个 D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】森林是地球之肺,每年能为人类提供大约28.3亿吨的有机物.28.3亿吨用科学记数法表示为( )
A.28.3×107
B.2.83×108
C.0.283×1010
D.2.83×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣2,﹣1,0,1,2,3,4的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a2﹣3a=0有实数根,且![]() 无解的概率是 .
无解的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com