
【题目】四边形ABCD内接于⊙O,AC为对角线,∠ACB=∠ACD
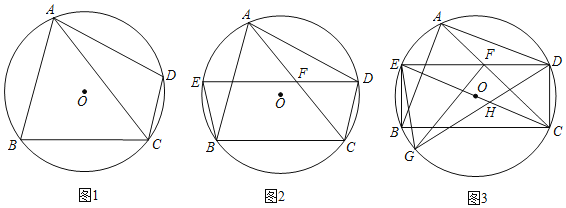
(1)如图1,求证:AB=AD;
(2)如图2,点E在AB弧上,DE交AC于点F,连接BE,BE=DF,求证:DF=DC;
(3)如图3,在(2)的条件下,点G在BC弧上,连接DG,交CE于点H,连接GE,GF,若DE=BC,EG=GH=5,S△DFG=9,求BC边的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图1,连接OA,OB,OD,由∠ACB=∠ACD,可得![]() ,可得AB=AD;
,可得AB=AD;
(2)连接AE,由“SAS”可证△ABE≌△ADF,可得∠BAE=∠DAC,可证BE=CD=DF;
(3)如图3,过点F作FN⊥GD于N,过点C作CM⊥GD于M,连接GC,通过证明△FDN≌△DCM,可得FN=DM,CM=DN,由面积公式可求FN=2,DM=2,DH=4,通过证明△EGC∽△DMC,△GEH∽△CHD,可得EC=![]() CD,CD2=
CD,CD2=![]() ,由勾股定理可求解.
,由勾股定理可求解.
证明:(1)如图1,连接OA,OB,OD,
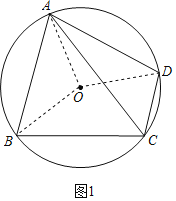
∵∠ACB=∠ACD,∠AOD=2∠ACD,∠AOB=2∠ACB
∴∠AOD=∠AOB
∴![]()
∴AD=AB;
(2)如图2,连接AE,
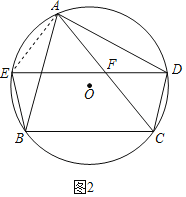
∵![]()
∴∠ABE=∠ADE
在△ABE和△ADF中

∴△ABE≌△ADF(SAS)
∴∠BAE=∠DAC
∴![]()
∴BE=DC
∵BE=DF
∴DF=DC;
(3)如图3,过点F作FN⊥GD于N,过点C作CM⊥GD于M,连接GC,
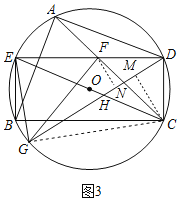
∵DE=BC,BE=CD,
∴四边形BCDE是平行四边形,
∴∠EBC=∠EDC,
∵四边形BEDC是圆内接四边形,
∴∠EBC+∠EDC=180°,
∴∠EDC=∠EBC=90°,
∴EC是直径,
∴∠FGC=∠EDC=90°
∴∠FDN+∠MDC=90°,且∠MDC+∠MCD=90°,
∴∠FDN=∠MCD,且∠FND=∠CMD=90°,DF=DC,
∴△FDN≌△DCM(AAS)
∴FN=DM,CM=DN,
∵EG=GH=5,
∴∠GEH=∠GHE,且∠GHE=∠DHC,∠GEH=∠GDC,
∴∠HDC=∠CHD,
∴CH=CD,且CM⊥DH,
∴DM=MH=FN,
∵S△DFG=9,
∴![]() DG×FN=9,
DG×FN=9,
∴![]() ×(5+2FN)×FN=9,
×(5+2FN)×FN=9,
∴FN=2,
∴DM=2,DH=4,
∵∠GEC=∠GDC,∠EGC=∠DMC,
∴△EGC∽△DMC,
∴![]() ,
,
∴EC=![]() CD,且HC=CD,
CD,且HC=CD,
∴EH=![]() CD,
CD,
∵∠EGD=∠ECD,∠GEC=∠GDC,
∴△GEH∽△CHD,
∴![]() ,
,
∴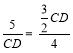 ,
,
∴![]() ,
,
∵EC2﹣CD2=DE2,
∴![]() ,
,
∴![]() ,
,
∴DE=![]()
∴BC=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
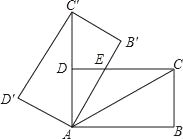
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A与原点O重合,顶点B在直线l上,将正方形沿射线OB方向无滑动地翻滚.若直线![]() ,正方形边长为2
,正方形边长为2![]()
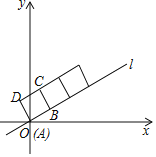
(1)翻滚后点A第一次落在直线l上的坐标是_____;
(2)当正方形翻滚2002次点A对应点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为![]() 的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程
的形式:求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为二元一次方程组来解;求解一元二次方程,把它转化为两个一元一次方程来解:求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想一一转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,解方程
,解方程![]() 和
和![]() ,可得方程
,可得方程![]() 的解.利用上述材料给你的启示,解下列方程;
的解.利用上述材料给你的启示,解下列方程;
(1)![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
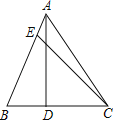
【题目】如图,在△ABC中,AD⊥BC于点D,点E在AB边上,连接CE,若∠BCE=2∠BAD,BE=2BD,AE:CD=3:8,S△ABC=39,则AC边的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鱼塘中养了某种鱼5000条,为了估计该鱼塘中该种鱼的总质量,从鱼塘中捕捞了3次,取得的数据如下:
数量/条 | 平均每条鱼的质量/kg | |
第1次捕捞 | 20 | 1.6 |
第2次捕捞 | 15 | 2.0 |
第3次捕捞 | 15 | 1.8 |
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为14元,求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数关系,并估计自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
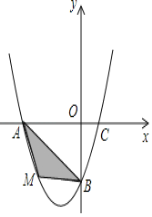
【题目】在平面直角坐标系中,已知抛物线经过A(﹣2,0),B(0,﹣2),C(1,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
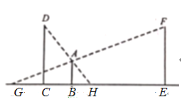
【题目】如图,一人站在两等高的路灯之间走动,![]() 为人
为人![]() 在路灯
在路灯![]() 照射下的影子,
照射下的影子,![]() 为人
为人![]() 在路灯
在路灯![]() 照射下的影子.当人从点
照射下的影子.当人从点![]() 走向点
走向点![]() 时两段影子之和
时两段影子之和![]() 的变化趋势是( )
的变化趋势是( )
A.先变长后变短B.先变短后变长
C.不变D.先变短后变长再变短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com