
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

【答案】![]()
【解析】试题解析:①如图1,当∠POQ=∠OAH=30°,若以P,O,Q为顶点的三角形与△AOH全等,那么A、P重合;
∵∠AOH=60°,
∴直线OA:y=![]() x,
x,
联立抛物线的解析式得: 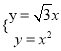 ,
,
解得: ![]() 或
或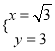 ,
,
故A(![]() ,3);
,3);
②当∠POQ=∠AOH=60°,此时△POQ≌△AOH,
易知∠POH=30°,则直线y=![]() x,联立抛物线的解析式,得:
x,联立抛物线的解析式,得: 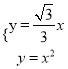 ,
,
解得: ![]() 或
或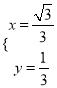 ,
,
故P(![]() ,
, ![]() ),那么A(
),那么A(![]() ,
, ![]() );
);
③当∠OPQ=90°,∠POQ=∠AOH=60°时,此时△QOP≌△AOH;
易知∠POH=30°,则直线y=![]() x,联立抛物线的解析式,得:
x,联立抛物线的解析式,得: 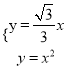 ,
,
解得: ![]() 或
或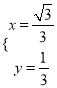 ,
,
故P(![]() ,
, ![]() ),
),
∴OP=![]() ,QP=
,QP=![]() ,
,
∴OH=OP=![]() ,AH=QP=
,AH=QP=![]() ,
,
故A(![]() ,
, ![]() );
);
④当∠OPQ=90°,∠POQ=∠OAH=30°,此时△OQP≌△AOH;
此时直线y=![]() x,联立抛物线的解析式,得:
x,联立抛物线的解析式,得:  ,
,
解得: ![]() 或
或 ,,
,,
∴P(![]() ,3),
,3),
∴QP=2,OP=2![]() ,
,
∴OH=QP=2,AH=OP=2![]() ,
,
故A(2,2![]() ).
).
综上可知:符合条件的点A有四个,分别为:(![]() ,3)或(
,3)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(2,2
)或(2,2![]() ).
).


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】下列说法中:①一个有理数不是正数就是负数;②射线AB和射线BA是同一条射线;③0的相反数是它本身;④两点之间,线段最短,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支架底端与桌面顶端的距离OA = 75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB =∠ACB = 37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37° ≈ 0.6,cos37°≈ 0.8,tan37° ≈ 0.75)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com