
ΓΨΧβΡΩΓΩ–ΓΝΝ‘Ύ―ßœΑ÷–”ωΒΫ’β―υ“ΜΗωΈ ΧβΘΚ
»γΆΦΘ§Βψ![]() «ΜΓ
«ΜΓ![]() …œ“ΜΕ·ΒψΘ§œΏΕΈ
…œ“ΜΕ·ΒψΘ§œΏΕΈ![]() Βψ
Βψ![]() «œΏΕΈ
«œΏΕΈ![]() ΒΡ÷–ΒψΘ§ΙΐΒψ
ΒΡ÷–ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() Θ§ΫΜ
Θ§ΫΜ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ°Β±
Θ°Β±![]() ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σœΏΕΈ
ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σœΏΕΈ![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°

–ΓΝΝΖ÷ΈωΖΔœ÷Θ§¥ΥΈ ΧβΚήΡ―Ά®Ιΐ≥ΘΙφΒΡΆΤάμΦΤΥψ≥ΙΒΉΫβΨωΘ§”Ύ «≥Δ ‘ΫαΚœ―ßœΑΚ· ΐΒΡΨ≠―ι―–ΨΩ¥ΥΈ ΧβΘ§«κΫΪœ¬ΟφΒΡΧΫΨΩΙΐ≥Χ≤Ι≥δΆξ’ϊΘΚ
![]() ΗυΨίΒψ
ΗυΨίΒψ![]() ‘ΎΜΓ
‘ΎΜΓ![]() …œΒΡ≤ΜΆ§ΈΜ÷ΟΘ§Μ≠≥ωœύ”ΠΒΡΆΦ–ΈΘ§≤βΝΩœΏΕΈ
…œΒΡ≤ΜΆ§ΈΜ÷ΟΘ§Μ≠≥ωœύ”ΠΒΡΆΦ–ΈΘ§≤βΝΩœΏΕΈ![]() ΒΡ≥ΛΕ»Θ§ΒΟΒΫœ¬±μΒΡΦΗΉιΕ‘”Π÷ΒΘ°
ΒΡ≥ΛΕ»Θ§ΒΟΒΫœ¬±μΒΡΦΗΉιΕ‘”Π÷ΒΘ°
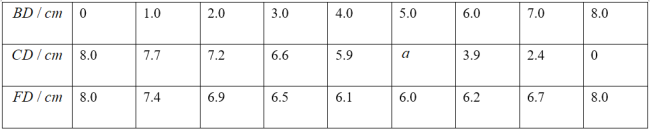
≤ΌΉς÷–ΖΔœ÷ΘΚ
ΔΌ"Β±Βψ![]() ΈΣΜΓ
ΈΣΜΓ![]() ΒΡ÷–Βψ ±Θ§
ΒΡ÷–Βψ ±Θ§ ![]() "Θ°‘ρ…œ÷–
"Θ°‘ρ…œ÷–![]() ΒΡ÷Β «
ΒΡ÷Β «
ΔΎ"œΏΕΈ![]() ΒΡ≥ΛΕ»Έό–η≤βΝΩΦ¥Ω…ΒΟΒΫ"Θ°«κΦρ“ΣΥΒΟςάμ”…ΘΜ
ΒΡ≥ΛΕ»Έό–η≤βΝΩΦ¥Ω…ΒΟΒΫ"Θ°«κΦρ“ΣΥΒΟςάμ”…ΘΜ
![]() ΫΪœΏΕΈ
ΫΪœΏΕΈ![]() ΒΡ≥ΛΕ»ΉςΈΣΉ‘±δΝΩ
ΒΡ≥ΛΕ»ΉςΈΣΉ‘±δΝΩ![]() ΚΆ
ΚΆ![]() ΒΡ≥ΛΕ»ΕΦ «
ΒΡ≥ΛΕ»ΕΦ «![]() ΒΡΚ· ΐΘ§Ζ÷±πΦ«ΈΣ
ΒΡΚ· ΐΘ§Ζ÷±πΦ«ΈΣ![]() ΚΆ
ΚΆ![]() Θ§≤Δ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ
Θ§≤Δ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Μ≠≥ωΝΥΚ· ΐ
÷–Μ≠≥ωΝΥΚ· ΐ![]() ΒΡΆΦœσΘ§»γΆΦΥυ ΨΘ°«κ‘ΎΆ§“ΜΉχ±ξœΒ÷–Μ≠≥ωΚ· ΐ
ΒΡΆΦœσΘ§»γΆΦΥυ ΨΘ°«κ‘ΎΆ§“ΜΉχ±ξœΒ÷–Μ≠≥ωΚ· ΐ![]() ΒΡΆΦœσΘΜ
ΒΡΆΦœσΘΜ
![]() ΦΧ–χ‘ΎΆ§“ΜΉχ±ξœΒ÷–Μ≠≥ωΥυ–ηΒΡΚ· ΐΆΦœσΘ§≤ΔΫαΚœΆΦœσ÷±Ϋ”–¥≥ωΘΚΒ±
ΦΧ–χ‘ΎΆ§“ΜΉχ±ξœΒ÷–Μ≠≥ωΥυ–ηΒΡΚ· ΐΆΦœσΘ§≤ΔΫαΚœΆΦœσ÷±Ϋ”–¥≥ωΘΚΒ±![]() ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§œΏΕΈ
ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§œΏΕΈ![]() ≥ΛΕ»ΒΡΫϋΥΤ÷ΒΘ°(ΫαΙϊ±ΘΝτ“ΜΈΜ–Γ ΐ)Θ°
≥ΛΕ»ΒΡΫϋΥΤ÷ΒΘ°(ΫαΙϊ±ΘΝτ“ΜΈΜ–Γ ΐ)Θ°
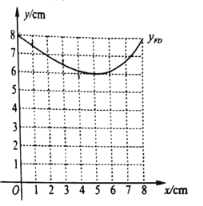
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ5.0ΘΜΔΎΦϊΫβΈωΘΜΘ®2Θ©ΆΦœσΦϊΫβΈωΘΜΘ®3Θ©ΆΦœσΦϊΫβΈωΘΜ3.5cmΜρ5.0cmΜρ6.3cmΘΜ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΒψ![]() ΈΣΜΓ
ΈΣΜΓ![]() ΒΡ÷–Βψ ±Θ§ΓςABDΓ’ΓςACDΘ§Φ¥Ω…ΒΟΒΫCD=BDΘΜΔΎ”…Χβ“βΒΟΓςACFΓ’ΓςABDΘ§Φ¥Ω…ΒΟΒΫCF=BDΘΜ
ΒΡ÷–Βψ ±Θ§ΓςABDΓ’ΓςACDΘ§Φ¥Ω…ΒΟΒΫCD=BDΘΜΔΎ”…Χβ“βΒΟΓςACFΓ’ΓςABDΘ§Φ¥Ω…ΒΟΒΫCF=BDΘΜ
Θ®2Θ©ΗυΨί±μΗώ ΐΨί‘Υ”ΟΟηΒψΖ®Φ¥Ω…Μ≠≥ωΚ· ΐΆΦœσΘΜ
Θ®3Θ©Μ≠≥ω![]() ΒΡΆΦœσΘ§Β±
ΒΡΆΦœσΘ§Β±![]() ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§Ζ÷«ιΩωΧ÷¬έΘ§»Έ“βΝΫ±ΏΖ÷±πœύΒ» ±Θ§Φ¥»Έ“βΝΫΗωΚ· ΐΆΦœσœύΫΜ ±ΒΡΫΜΒψΚαΉχ±ξΦ¥ΈΣBDΒΡΫϋΥΤ÷ΒΘ°
ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§Ζ÷«ιΩωΧ÷¬έΘ§»Έ“βΝΫ±ΏΖ÷±πœύΒ» ±Θ§Φ¥»Έ“βΝΫΗωΚ· ΐΆΦœσœύΫΜ ±ΒΡΫΜΒψΚαΉχ±ξΦ¥ΈΣBDΒΡΫϋΥΤ÷ΒΘ°
ΫβΘΚΘ®1Θ©ΔΌΒψ![]() ΈΣΜΓ
ΈΣΜΓ![]() ΒΡ÷–Βψ ±Θ§”…‘≤ΒΡ–‘÷ Ω…ΒΟΘΚ
ΒΡ÷–Βψ ±Θ§”…‘≤ΒΡ–‘÷ Ω…ΒΟΘΚ
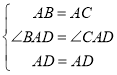 Θ§
Θ§
ΓύΓςABDΓ’ΓςACDΘ§
ΓύCD=BD=5.0Θ§
Γύ![]() ΘΜ
ΘΜ
ΔΎΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏ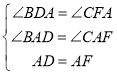 Θ§
Θ§
ΓύΓςACFΓ’ΓςABDΘ§
ΓύCF=BDΘ§
ΓύœΏΕΈ![]() ΒΡ≥ΛΕ»Έό–η≤βΝΩΦ¥Ω…ΒΟΒΫΘΜ
ΒΡ≥ΛΕ»Έό–η≤βΝΩΦ¥Ω…ΒΟΒΫΘΜ
Θ®2Θ©Κ· ΐ![]() ΒΡΆΦœσ»γΆΦΥυ ΨΘΚ
ΒΡΆΦœσ»γΆΦΥυ ΨΘΚ
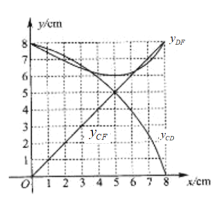
Θ®3Θ©”…Θ®1Θ©÷Σ![]() Θ§
Θ§
Μ≠≥ω![]() ΒΡΆΦœσΘ§»γ…œΆΦΥυ ΨΘ§Β±
ΒΡΆΦœσΘ§»γ…œΆΦΥυ ΨΘ§Β±![]() ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§
ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§
ΔΌ![]() Θ§BDΈΣ
Θ§BDΈΣ![]() ”κ
”κ![]() Κ· ΐΆΦœσΒΡΫΜΒψΚαΉχ±ξΘ§Φ¥BD=5.0cmΘΜ
Κ· ΐΆΦœσΒΡΫΜΒψΚαΉχ±ξΘ§Φ¥BD=5.0cmΘΜ
ΔΎ![]() Θ§BDΈΣ
Θ§BDΈΣ![]() ”κ
”κ![]() Κ· ΐΆΦœσΒΡΫΜΒψΚαΉχ±ξΘ§Φ¥BD=6.3cmΘΜ
Κ· ΐΆΦœσΒΡΫΜΒψΚαΉχ±ξΘ§Φ¥BD=6.3cmΘΜ
Δέ![]() Θ§BDΈΣ
Θ§BDΈΣ![]() ”κ
”κ![]() Κ· ΐΆΦœσΒΡΫΜΒψΚαΉχ±ξΘ§Φ¥BD=3.5cmΘΜ
Κ· ΐΆΦœσΒΡΫΜΒψΚαΉχ±ξΘ§Φ¥BD=3.5cmΘΜ
Ήέ…œΘΚΒ±![]() ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§œΏΕΈ
ΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§œΏΕΈ![]() ≥ΛΕ»ΒΡΫϋΥΤ÷ΒΈΣ3.5cmΜρ5.0cmΜρ6.3cmΘ°
≥ΛΕ»ΒΡΫϋΥΤ÷ΒΈΣ3.5cmΜρ5.0cmΜρ6.3cmΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆ®ΙΐΩΈ±Ψ…œΕ‘Κ· ΐΒΡ―ßœΑΘ§Έ“Ο«ΜΐάέΝΥ“ΜΕ®ΒΡΨ≠―ιΘ§œ¬±μ «“ΜΗωΚ· ΐΒΡΉ‘±δΝΩ![]() ”κΚ· ΐ÷Β
”κΚ· ΐ÷Β![]() ΒΡ≤ΩΖ÷Ε‘”Π÷ΒΘ§«κΡψΫηΦχ“‘Άυ―ßœΑΚ· ΐΒΡΨ≠―ιΘ§ΧΫΨΩœ¬Ν–Έ ΧβΘΚ
ΒΡ≤ΩΖ÷Ε‘”Π÷ΒΘ§«κΡψΫηΦχ“‘Άυ―ßœΑΚ· ΐΒΡΨ≠―ιΘ§ΧΫΨΩœ¬Ν–Έ ΧβΘΚ
| Γ≠ | 0 | 1 | 2 | 3 | 4 | 5 | Γ≠ |
| Γ≠ | 6 | 3 | 2 | 1.5 | 1.2 | 1 | Γ≠ |
Θ®1Θ©Β±![]() ±Θ§
±Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©ΗυΨί±μ÷– ΐ÷ΒΟηΒψ![]() Θ§≤ΔΜ≠≥ωΚ· ΐΆΦœσΘΜ
Θ§≤ΔΜ≠≥ωΚ· ΐΆΦœσΘΜ
Θ®3Θ©Ιέ≤λΜ≠≥ωΒΡΆΦœσΘ§–¥≥ω’βΗωΚ· ΐΒΡ“ΜΧθ–‘÷ ΘΚ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
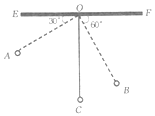
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΒψAΘ®5Θ§3Θ©Θ§ΒψBΘ®©¹3Θ§3Θ©Θ§ΙΐΒψAΒΡ÷±œΏyΘΫ![]() x+mΘ®mΈΣ≥Θ ΐΘ©”κ÷±œΏxΘΫ1ΫΜ”ΎΒψPΘ§”κx÷αΫΜ”ΎΒψCΘ§÷±œΏBP”κx÷αΫΜ”ΎΒψDΘ°
x+mΘ®mΈΣ≥Θ ΐΘ©”κ÷±œΏxΘΫ1ΫΜ”ΎΒψPΘ§”κx÷αΫΜ”ΎΒψCΘ§÷±œΏBP”κx÷αΫΜ”ΎΒψDΘ°
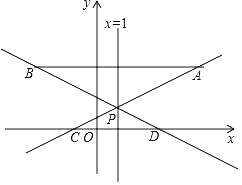
Θ®1Θ©«σΒψPΒΡΉχ±ξΘΜ
Θ®2Θ©«σ÷±œΏBPΒΡΫβΈω ΫΘ§≤Δ÷±Ϋ”–¥≥ωΓςPCD”κΓςPABΒΡΟφΜΐ±»ΘΜ
Θ®3Θ©»τΖ¥±»άΐΚ· ΐ![]() Θ®kΈΣ≥Θ ΐ«“kΓΌ0Θ©ΒΡΆΦœσ”κœΏΕΈBD”–ΙΪΙ≤Βψ ±Θ§«κ÷±Ϋ”–¥≥ωkΒΡΉν¥σ÷ΒΜρΉν–Γ÷ΒΘ°
Θ®kΈΣ≥Θ ΐ«“kΓΌ0Θ©ΒΡΆΦœσ”κœΏΕΈBD”–ΙΪΙ≤Βψ ±Θ§«κ÷±Ϋ”–¥≥ωkΒΡΉν¥σ÷ΒΜρΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗυΨίαι÷ί –Ά≥ΦΤΨ÷ΖΔ≤ΦΒΡΆ≥ΦΤ ΐΨίœ‘ ΨΘ§αι÷ί –Ϋϋ5ΡξΙζΟώ…ζ≤ζΉή÷Β ΐΨί»γΆΦ1Υυ ΨΘ§2016ΡξΙζΟώ…ζ≤ζΉή÷Β÷–ΒΎ“Μ≤ζ“ΒΓΔΒΎΕΰ≤ζ“ΒΓΔΒΎ»ΐ≤ζ“ΒΥυ’Φ±»άΐ»γΆΦ2Υυ ΨΓΘ
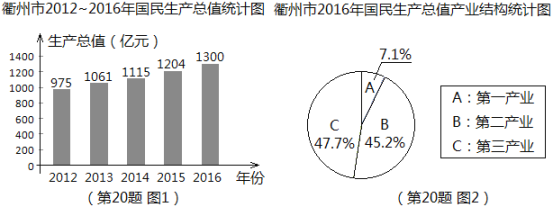
«κΗυΨίΆΦ÷––≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«σ2016ΡξΒΎ“Μ≤ζ“Β…ζ≤ζΉή÷ΒΘ®ΨΪ»ΖΒΫ1“Ύ‘ΣΘ©ΘΜ
Θ®2Θ©2016Ρξ±»2015ΡξΒΡΙζΟώ…ζ≤ζΉή÷Β‘ωΦ”ΝΥΑΌΖ÷÷°ΦΗΘ®ΨΪ»ΖΒΫ1%Θ©ΘΩ
Θ®3Θ©»τ“Σ Ι2018ΡξΒΡΙζΟώ…ζ≤ζΉή÷Β¥οΒΫ1573“Ύ‘ΣΘ§«σ2016Ρξ÷Ν2018ΡξΈ“ –ΙζΟώ…ζ≤ζΉή÷ΒΤΫΨυΡξ‘ω≥Λ¬ Θ®ΨΪ»ΖΒΫ1%Θ©ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΖΔ’Ιœγ¥εΨ≠ΦΟΘ§Ρ≥¥εΗυΨί±ΨΒΊΧΊ…ΪΘ§¥¥ΑλΝΥ…Ϋ“©ΖέΦ”ΙΛ≥ßΘ°ΗΟ≥ß–ηΙΚ÷Ο“ΜΧ®Ζ÷ΉΑΜζΘ§ΦΤΜ°¥”…ΧΦ“ΆΤΦω ‘”ΟΒΡΦΉΓΔ““ΝΫΧ®≤ΜΆ§ΤΖ≈ΤΒΡΖ÷ΉΑΜζ÷–―Γ‘ώΘ° ‘”Ο ±Θ§…ηΕ®Ζ÷ΉΑΒΡ±ξΉΦ÷ ΝΩΈΣΟΩ¥ϋ![]() Θ§”κ÷°œύ≤ν¥σ”Ύ
Θ§”κ÷°œύ≤ν¥σ”Ύ![]() ΈΣ≤ΜΚœΗώΘ°ΈΣΦλ―ιΖ÷ΉΑ–ßΙϊΘ§ΙΛ≥ßΕ‘’βΝΫΧ®ΜζΤςΖ÷ΉΑΒΡ≥…ΤΖΫχ––ΝΥ≥ι―υΚΆΖ÷ΈωΘ§Ιΐ≥Χ»γœ¬ΘΚ
ΈΣ≤ΜΚœΗώΘ°ΈΣΦλ―ιΖ÷ΉΑ–ßΙϊΘ§ΙΛ≥ßΕ‘’βΝΫΧ®ΜζΤςΖ÷ΉΑΒΡ≥…ΤΖΫχ––ΝΥ≥ι―υΚΆΖ÷ΈωΘ§Ιΐ≥Χ»γœ¬ΘΚ
[ ’Φ· ΐΨί]¥”ΦΉΓΔ““ΝΫΧ®ΜζΤςΖ÷ΉΑΒΡ≥…ΤΖ÷–ΗςΥφΜζ≥ι»Γ![]() ¥ϋΘ§≤βΒΟ ΒΦ ÷ ΝΩ(ΒΞΈΜΘΚ
¥ϋΘ§≤βΒΟ ΒΦ ÷ ΝΩ(ΒΞΈΜΘΚ![]() )
)
»γœ¬ΘΚ
ΦΉΘΚ ![]()
““ΘΚ![]()
[’ϊάμ ΐΨί]’ϊάμ“‘…œ ΐΨίΘ§ΒΟΒΫΟΩ¥ϋ÷ ΝΩ![]() ΒΡΤΒ ΐΖ÷≤Φ±μΘ°
ΒΡΤΒ ΐΖ÷≤Φ±μΘ°

[Ζ÷Έω ΐΨί]ΗυΨί“‘…œ ΐΨίΘ§ΒΟΒΫ“‘œ¬Ά≥ΦΤΝΩΘ°

ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
![]() ±μΗώ÷–ΒΡ
±μΗώ÷–ΒΡ![]()
![]()
![]() ΉέΚœ…œ±μ÷–ΒΡΆ≥ΦΤΝΩΘ§≈–ΕœΙΛ≥ß”Π―ΓΙΚΡΡ“ΜΧ®Ζ÷ΉΑΜζΘ§≤ΔΥΒΟςάμ”…Θ°
ΉέΚœ…œ±μ÷–ΒΡΆ≥ΦΤΝΩΘ§≈–ΕœΙΛ≥ß”Π―ΓΙΚΡΡ“ΜΧ®Ζ÷ΉΑΜζΘ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
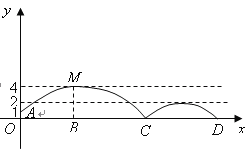
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΈοάμΫΧ ΠΈΣΆ§―ßΟ«―ί ΨΒΞΑΎ‘ΥΕ·Θ§ΒΞΑΎΉσ”“ΑΎΕ·÷–Θ§‘Ύ![]() ΒΡΈΜ÷Ο ±Η©Ϋ«
ΒΡΈΜ÷Ο ±Η©Ϋ«![]() Θ§‘Ύ
Θ§‘Ύ![]() ΒΡΈΜ÷Ο ±Η©Ϋ«
ΒΡΈΜ÷Ο ±Η©Ϋ«![]() Θ§»τ
Θ§»τ![]() Θ§Βψ
Θ§Βψ![]() ±»Βψ
±»Βψ![]() ΗΏ7
ΗΏ7![]() Θ°
Θ°
«σΘΚΘ®1Θ©ΒΞΑΎΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©¥”Βψ![]() ΑΎΕ·ΒΫΒψ
ΑΎΕ·ΒΫΒψ![]() Ψ≠ΙΐΒΡ¬ΖΨΕ≥ΛΘ°Θ®“Σ«σΘΚ±ΨΧβ÷–ΒΡΦΤΥψΫαΙϊΨυ±ΘΝτ’ϊ ΐΘ°≤ΈΩΦ÷ΒΘΚ
Ψ≠ΙΐΒΡ¬ΖΨΕ≥ΛΘ°Θ®“Σ«σΘΚ±ΨΧβ÷–ΒΡΦΤΥψΫαΙϊΨυ±ΘΝτ’ϊ ΐΘ°≤ΈΩΦ÷ΒΘΚ![]() ΘΜ
ΘΜ![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ήψ«ρ≥Γ…œ ΊΟ≈‘±‘Ύ![]() ¥ΠΩΣ≥ω“ΜΗΏ«ρΘ§«ρ¥”άκΒΊΟφ1ΟΉΒΡ
¥ΠΩΣ≥ω“ΜΗΏ«ρΘ§«ρ¥”άκΒΊΟφ1ΟΉΒΡ![]() ¥ΠΖ…≥ωΘ®
¥ΠΖ…≥ωΘ®![]() ‘Ύ
‘Ύ![]() ÷α…œΘ©Θ§‘ΥΕ·‘±““‘ΎΨύ
÷α…œΘ©Θ§‘ΥΕ·‘±““‘ΎΨύ![]() Βψ6ΟΉΒΡ
Βψ6ΟΉΒΡ![]() ¥ΠΖΔœ÷«ρ‘ΎΉ‘ΦΚΆΖΒΡ’ΐ…œΖΫ¥οΒΫΉνΗΏΒψ
¥ΠΖΔœ÷«ρ‘ΎΉ‘ΦΚΆΖΒΡ’ΐ…œΖΫ¥οΒΫΉνΗΏΒψ![]() Θ§ΨύΒΊΟφ‘Φ4ΟΉΗΏΘ§«ρ¬δΒΊΚσ”÷“Μ¥ΈΒ·ΤπΘ°Ψί Β―ι≤βΥψΘ§Ήψ«ρ‘Ύ≤ίΤΚ…œΒ·ΤπΚσΒΡ≈ΉΈοœΏ”κ‘≠ά¥ΒΡ≈ΉΈοœΏ–ΈΉ¥œύΆ§Θ§Ήν¥σΗΏΕ»Φθ…ΌΒΫ‘≠ά¥Ήν¥σΗΏΕ»ΒΡ“ΜΑκΘ°
Θ§ΨύΒΊΟφ‘Φ4ΟΉΗΏΘ§«ρ¬δΒΊΚσ”÷“Μ¥ΈΒ·ΤπΘ°Ψί Β―ι≤βΥψΘ§Ήψ«ρ‘Ύ≤ίΤΚ…œΒ·ΤπΚσΒΡ≈ΉΈοœΏ”κ‘≠ά¥ΒΡ≈ΉΈοœΏ–ΈΉ¥œύΆ§Θ§Ήν¥σΗΏΕ»Φθ…ΌΒΫ‘≠ά¥Ήν¥σΗΏΕ»ΒΡ“ΜΑκΘ°
Θ®1Θ©«σΉψ«ρΩΣ ΦΖ…≥ωΒΫΒΎ“Μ¥Έ¬δΒΊ ±Θ§ΗΟ≈ΉΈοœΏΒΡ±μ¥ο ΫΘ°
Θ®2Θ©Ήψ«ρΒΎ“Μ¥Έ¬δΒΊΒψ![]() Ψύ ΊΟ≈‘±Εύ…ΌΟΉΘΩΘ®»Γ
Ψύ ΊΟ≈‘±Εύ…ΌΟΉΘΩΘ®»Γ![]() Θ©
Θ©
Θ®3Θ©‘ΥΕ·‘±“““Σ«άΒΫΒΎΕΰΗω¬δΒψ![]() Θ§Υϊ”Π‘Όœρ«Α≈ήΕύ…ΌΟΉΘΩ
Θ§Υϊ”Π‘Όœρ«Α≈ήΕύ…ΌΟΉΘΩ
Θ®»Γ![]() Θ©
Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com