
分析 (1)利用二次根式的性质结合负整数指数幂的性质和特殊角的三角函数值、绝对值的性质分别化简求出答案;
(2)利用零指数幂的性质结合负整数指数幂的性质和特殊角的三角函数值分别化简求出答案.
解答 解:(1)$\sqrt{12}$-($\frac{1}{2}$)-1-|1-$\sqrt{3}$|+2sin30°
=2$\sqrt{3}$-2-($\sqrt{3}$-1)+1
=$\sqrt{3}$;
(2)2-1-(π-2014)0+cos245°+tan30°•sin60°
=$\frac{1}{2}$-1+($\frac{\sqrt{2}}{2}$)2+$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$.
点评 此题主要考查了实数运算,正确化简各数是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
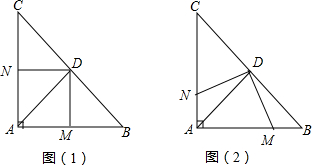 在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.
在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com