
【题目】已知关于x的二次函数y=ax2﹣4ax+a+1(a>0)
(1)若二次函数的图象与x轴有交点,求a的取值范围;
(2)若P(m,n)和Q(5,b)是抛物线上两点,且n>b,求实数m的取值范围;
(3)当m≤x≤m+2时,求y的最小值(用含a、m的代数式表示).
【答案】(1)a≥![]() ;(2)m<﹣1或m>5;(3)y的最小值为:am2﹣3a+1或﹣3a+1或am2﹣4am+a+1.
;(2)m<﹣1或m>5;(3)y的最小值为:am2﹣3a+1或﹣3a+1或am2﹣4am+a+1.
【解析】
(1)令对应一元二次方程根的判别式大于等于0,然后解答即可;
(2)根据抛物线的对称轴为直线x=![]() ,当n=b时,根据函数的对称性,可得m=-1,最后确定m的取值范围即可;
,当n=b时,根据函数的对称性,可得m=-1,最后确定m的取值范围即可;
(3)分m<0,0≤m≤2,m>2三种情况别求解即可.
解:(1)由题意得:
△=(﹣4a)2﹣4a(a+1)≥0,且a>0,
解得:a≥![]() ;
;
(2)抛物线的对称轴为直线x=﹣![]() =2,
=2,
当n=b时,根据函数的对称性,则m=﹣1或m=5,
故实数m的取值范围为:m<﹣1或m>5;
(3)①当m+2<2时,即m<0时,
函数在x=m+2时,取得最小值,
ymin=a(m+2)2﹣4a(m+2)+a+1=am2﹣3a+1;
②当m≤2≤m+2时,即0≤m≤2,
函数在顶点处取得最小值,
即ymin=4a﹣4a×2+a+1=﹣3a+1;
③当m>2时,
函数在x=m时,取得最小值,
ymin=am2﹣4am+a+1;
综上,y的最小值为:am2﹣3a+1或﹣3a+1或am2﹣4am+a+1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
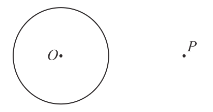
【题目】下面是小文设计的“过圆外一点作圆的切线”的作图过程.已知:![]() 和圆外一点
和圆外一点![]() .求作:过点
.求作:过点![]() 的
的![]() 的切线.作法:①连接
的切线.作法:①连接![]() ;②以
;②以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ;③作直线
;③作直线![]() ,
,![]() ;所以直线
;所以直线![]() ,
,![]() 为
为![]() 的切线.
的切线.
根据小文设计的作图过程,完成下面的证明.
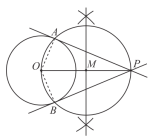
证明:连接![]() ,
,![]() .
.
∵![]() 为
为![]() 的直径,
的直径,
∴![]() =∠________=________
=∠________=________
(________)(填推理的依据).
∴![]() ,________
,________![]() .
.
∵![]() ,
,![]() 为
为
∴直线![]() ,
,![]() 为
为![]() 的切线(________)(填推理的依据).
的切线(________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 在平面直角坐标系
在平面直角坐标系![]() 中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点
中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点![]() 的坐标是( )
的坐标是( )
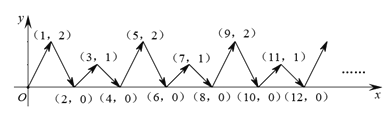
A.(26,0)B.(26,1)C.(27,1)D.(27,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,六边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
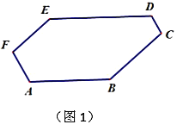
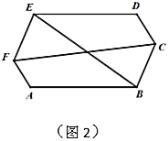
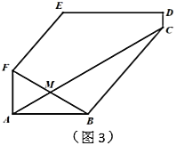
(1)找出这个六边形中所有相等的内角_______.证明其中的一个结论.
(2)如果![]() ,证明对角线
,证明对角线![]() ,
,![]() 互相平分;
互相平分;
(3)如图,如果![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分对角线
平分对角线![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
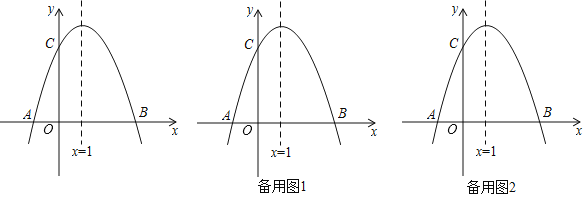
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对该校学生进行了“你喜欢的运动项目”的情况问卷调查,在全部调查问卷中,随机抽取了部分学生的调查问卷进行了分析整理,得到了如下的样本统计图表和扇形统计图:
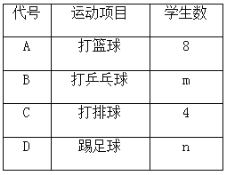
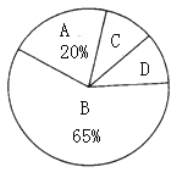
(1)求m,n的值;
(2)该校学生总数为500人,学校决定按比例在B,C,D类学生中抽取学生进行课余训练,其比例为B类20%,C,D类各取60%,请你估计该校参加课余训练的学生数;
(3)随机抽取的部分学生的调查问卷中,若C类运动项目的4位学生中有3位男生,1位女生,请用列举法求出在C类中随机抽出2位学生进行专家培训,其中有1位女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坚持节约资源和保护环境是我国的基本国策,国家要求加强生活垃圾分类回收与再生资源回收有效衔接,提高全社会资源产出率,构建全社会的资源循环利用体系.
图1反映了2014—2019年我国生活垃圾清运量的情况.

图2反映了2019年我国G市生活垃圾分类的情况.
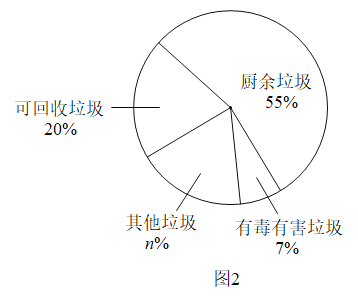
根据以上材料回答下列问题:
(1)图2中,n的值为___________;
(2)2014—2019年,我国生活垃圾清运量的中位数是_________;
(3)据统计,2019年G市清运的生活垃圾中可回收垃圾约为0.02亿吨,所创造的经济总价值约为40亿元.若2019年我国生活垃圾清运量中,可回收垃圾的占比与G市的占比相同,根据G市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com