

分析 (1)设字距为xcm,则边空宽为3xcm,字宽为4xcm,根据显示屏的总长度为900cm,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据边空宽:字宽:字距=3:4:1可找出边空宽及字距,设字数为y个,根据显示屏的总长度为900cm,即可得出关于y的一元一次方程,解之即可得出结论.
解答 解:(1)设字距为xcm,则边空宽为3xcm,字宽为4xcm,
根据题意得:(17-1)x+2×3x+17×4x=900,
解得:x=10.
答:某次活动的字数为17个,字距是10cm.
(2)设字数为y个,
根据题意得:45y+2×$\frac{3}{4}$×45+$\frac{1}{4}$×45(y-1)=900,
解得:y=15.
答:字数总共是15个.
点评 本题考查了一元一次方程的应用,解题的关键是:(1)根据显示屏的总长度为900cm,列出关于x的一元一次方程;(2)根据显示屏的总长度为900cm,列出关于y的一元一次方程.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
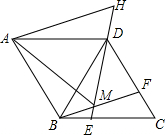 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形④S四边形ABMD=$\frac{\sqrt{3}}{4}$AM2.
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形④S四边形ABMD=$\frac{\sqrt{3}}{4}$AM2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
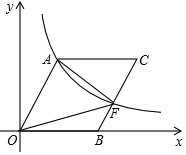 如图,O为坐标原点,点B在x轴上,四边形OACB为平行四边形,cos∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}(k>0)$在第一象限内的图象经过点A,与BC交于点F.
如图,O为坐标原点,点B在x轴上,四边形OACB为平行四边形,cos∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}(k>0)$在第一象限内的图象经过点A,与BC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
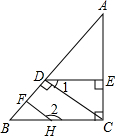 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,并说明理由(填空)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com