
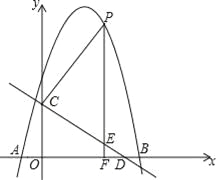
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬ֱ��y=��![]() x+3��y�ύ�ڵ�C����x�ύ�ڵ�D����P��x���Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
x+3��y�ύ�ڵ�C����x�ύ�ڵ�D����P��x���Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
��1���������ߵĽ���ʽ��
��2����PE=5EF����m��ֵ��
��3������E���ǵ�E����ֱ��PC�ĶԳƵ㡢�Ƿ���ڵ�P��ʹ��E������y���ϣ������ڣ���ֱ��д����Ӧ�ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2+4x+5����2��m=2��m=![]() ��
��
��3�����ɼ�����.
�������������������1�����ô���ϵ������������ߵĽ���ʽ��
��2���ú�m�Ĵ���ʽ�ֱ��ʾ��PE��EF��Ȼ���з�����⣻
��3������ؼ���ʶ������ı���PECE�������Σ�Ȼ�����PE=CE���������г�������⣻���ı���PECE�������β�����ʱ��P��y���ϣ����ɵõ���P���꣮
�����������1����������y=��x2+bx+c��x�ύ��A ����1��0����B��5��0�����㣬
��![]() ���
���![]() ��
��
�������ߵĽ���ʽΪy=��x2+4x+5��
��2������P�ĺ�����Ϊm��
��P��m����m2+4m+5����E��m����![]() m+3����F��m��0����
m+3����F��m��0����
��PE=|yP��yE|=|����m2+4m+5��������![]() m+3��|=|��m2+
m+3��|=|��m2+![]() m+2|��
m+2|��
EF=|yE��yF|=|����![]() m+3����0|=|��
m+3����0|=|��![]() m+3|��
m+3|��
�����⣬PE=5EF������|��m2+![]() m+2|=5|��
m+2|=5|��![]() m+3|=|��
m+3|=|��![]() m+15|
m+15|
������m2+![]() m+2=��
m+2=��![]() m+15�������ã�2m2��17m+26=0��
m+15�������ã�2m2��17m+26=0��
��ã�m=2��m=![]() ��
��
������m2+![]() m+2=������
m+2=������![]() m+15���������ã�m2��m��17=0��
m+15���������ã�m2��m��17=0��
��ã�m=![]() ��m=
��m=![]() ��
��
�����⣬m��ȡֵ��ΧΪ����1��m��5����m=![]() ��m==
��m==![]() �����������ȥ��
�����������ȥ��
��m=2��m=![]() ��
��
��3��������ڣ�
����ʾ��ͼ���£�
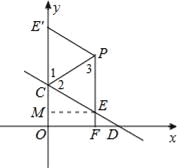
����E��E������ֱ��PC�Գƣ�
���1=��2��CE=CE����PE=PE����
��PEƽ����y�ᣬ���1=��3��
���2=��3����PE=CE��
��PE=CE=PE��=CE�������ı���PECE�������Σ�
���ı���PECE�������δ���ʱ��
��ֱ��CD����ʽy=��![]() x+3���ɵ�OD=4��OC=3���ɹ��ɶ�����CD=5��
x+3���ɵ�OD=4��OC=3���ɹ��ɶ�����CD=5��
����E��EM��x�ᣬ��y���ڵ�M������CEM�ס�CDO��
��![]() =
=![]() =����
=����![]() =
=![]() �����CE=
�����CE=![]() |m|��
|m|��
��PE=CE=![]() |m|�����ɣ�2����֪��PE=|��m2+
|m|�����ɣ�2����֪��PE=|��m2+![]() m+2|
m+2|
��|��m2+![]() m+2|=
m+2|=![]() |m|��
|m|��
������m2+![]() m+2=
m+2=![]() m�������ã�2m2��7m��4=0�����m=4��m=��
m�������ã�2m2��7m��4=0�����m=4��m=��![]() ��
��
������m2+![]() m+2=��
m+2=��![]() m�������ã�m2��6m��2=0�����m1=3+
m�������ã�m2��6m��2=0�����m1=3+![]() ��m2=3��
��m2=3��![]() ��
��
�����⣬m��ȡֵ��ΧΪ����1��m��5����m=3+![]() �������ȥ��
�������ȥ��
���ı���PECE����������һ����������ʱ��
��ʱP�������Ϊ0��E��C��E'�����غ���y���ϣ�Ҳ�������⣬
��P��0��5��
�����������������������ĵ�P����Ϊ��0��5������![]() ��
��![]() ����4��5����3��
����4��5����3��![]()
2![]() ��3����
��3����


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
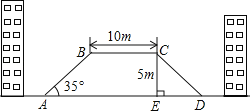
����Ŀ����ͼ��Ϊ�˻��⽻ͨӵ�£��������ˣ���ij�ֵ��ƻ���һ�������Ϊ����ABCD�Ĺ������ţ�������б��AB���½���BADΪ35�㣬б��CD���¶�Ϊi=1��1.2����ֱ�߶�CE��ˮƽ����DE�ıȣ����ϵ�BC=10m�����Ÿ߶�CE=5m���������µ�AD�ij��ȣ��������ȷ��0.1m���ο����ݣ�sin35���0.57��cos35���0.82��tan35���0.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��BC��BD��AD��AC ��BD ����O��AC=BD��
��֤����1��BC=AD��
��2����OAB�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥AB�Ҳ���һ�ϰ�����ϰ�����Ա���һ��С¥DE����С¥�Ķ���D������ϰ����Ե��C�ĸ���Ϊ30�㣬��ô�¥����A������Ϊ45�㣨��B��C��E��ͬһˮƽֱ���ϣ�����֪AB=80 m��DE=10 m�����ϰ���B��C�����ľ��룮(�����ȷ��0.1 m)���ο����ݣ� ![]() ��1.414����
��1.414����![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x+y=2��xy=��2����1��x����1��y����ֵΪ�� ��
A.��1
B.1
C.5
D.��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC������ACB��90����AC��BC����ABC�ĸ�CD���ƽ����AE�ཻ��F������C��CH��AE��G����AB��H��
��1������BCH�Ķ�����
��2����֤��CE��BH��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������ҪmԪ����һ��������ҪnԪ������4�������7��������Ҫ����Ԫ�� ��
A.4m+7nB.28mnC.7m+4nD.11mn
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
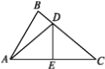
����Ŀ����ͼ����֪��BAC=60�� ,��B=80�� ,DE��ֱƽ��AC��BC�ڵ�D,��AC�ڵ�E.
(1)���BAD�Ķ�����
(2)��AB=10,BC=12,����ABD���ܳ�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com