Question

如图①，在Rt△ABC中，∠BAC=90°，AB=AC=，D、E两点分别在AC、BC上，且DE∥AB，CD=．将△CDE绕点C顺时针旋转，得到△CD′E′（如图②，点D′、E′分别与点D、E对应），点E′在AB上，D′E′与AC相交于点M．
（1）求∠ACE′的度数；
（2）求证：四边形ABCD′是梯形；
（3）求△AD′M的面积．

Answer 1

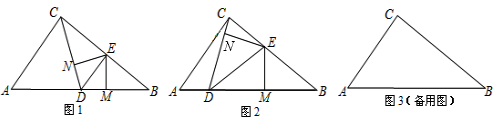
（1）解：如图1，∵∠BAC=90°，AB=AC，
∴∠B=∠ACB=45°，
∵DE∥AB，
∴∠DEC=∠DCE=45°，∠EDC=90°，
∴DE=CD=2，
∴CE=CE′=4．
如图2，在Rt△ACE′中，∠E′AC=90°，AC=2，CE′=4，
∴cos∠ACE′=
∴∠ACE′=30°．

（2）证明：如图2，∠D′CE′=∠ACB=45°，∠ACE′=30°，
∴∠D′CA=∠E′CB=15°，
又，
∴△D′CA∽△E′CB．
∴∠D′AC=∠B=45°，
∴∠ACB=∠D′AC，
∴AD′∥BC．
∵∠B=45°，∠D′CB=60°，
∴∠ABC与∠D′CB不互补，
∴AB与D′C不平行．
∴四边形ABCD′是梯形．

（3）解：在图②中，过点C作CF⊥AD′，垂足为F．
∵AD′∥BC，
∴CF⊥BC．
∴∠FCD′=∠ACF-∠ACD′=30°．
在Rt△ACF中，AF=CF=，
∴S_△ACF=3，
在Rt△D′CF中，CD′=2，∠FCD′=30°，
∴D′F=，
∴S_△D′CF=．
同理，S_Rt△AE′C=2，S_{Rt△D′E′C}=4．
∵∠AME′=∠D′MC，∠E′AM=∠CD′M，
∴△AME′∽△D′MC．．

①∴S_△AE′M=S_△CD′M．
②∵S_△EMC+S_△AE′M=S_△AE′C=2，
③S_△E′MC+S_△CD′M=S_△D′EC=4．
由③-②，得S_△C′DM-S_△AE′M=4-2，
由①，得S_△CD′M=8-4，
∴S_△AD′M=S_△ACF-S_△DCF-S_△CD′M=3-5．
∴△AD′M的面积是-5．
分析：（1）根据已知条件容易知道△EDC是等腰直角三角形，也容易求出CE，然后在Rt△ACE′解直角三角形就可以求出∠ACE，
（2）根据（1）的结论和已知条件可以证明△D′CA∽△E′CB，再利用相似三角形的性质就可以证明四边形ABCD′是梯形；
（3）AD′M的面积不能直接求出，要采用面积的割补法，首先确定S_△AD′M=S_△ACF-S_△DCF-S_△CD′M，然后分别求出
它们的面积，其中求S_△C′DM比较复杂，还要利用相似三角形的面积的比等于相似比的平方这个结论，最后才能求出△AD′M的面积．
点评：此题综合性比较强，难度比较大，考查的知识点比较多，有等腰直角三角形的性质、相似三角形的性质与判定、面积的割补法和解直接三角形等．