方程3x+y=7.用x的代数式表示y.则y=-3x+7．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

16．方程3x+y=7，用x的代数式表示y，则y=-3x+7．

分析把x看做已知数求出y即可．

解答解：方程3x+y=7，
解得：y=-3x+7，
故答案为：-3x+7

点评此题考查了解二元一次方程，解题的关键是将x看做已知数求出y．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

6．

已知y是x的函数，自变量x的取值范围是x＞0，下表是y与x的几组对应值．

x	…	1	2	4	5	6	8	9	…
y	…	3.92	1.95	0.98	0.78	2.44	2.44	0.78	…

小风根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象和性质进行了探究．
下面是小风的探究过程，请补充完整：
（1）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（2）根据画出的函数图象，写出：
①x=7对应的函数值y约为3.0．
②该函数的一条性质：该函数没有最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

某中学为了解学生到校交通方式情况，随机抽取各年级部分学生就“上下学交通方式”进行问卷调查，调查分为“A：骑自行车；B：不行；C：坐公交车；D：其他”四种情况，并根据调查结果绘制出部分条形统计图（如图1）和部分扇形统计图（如图2），请根据图中的信息，解答下列问题：
（1）本次调查共抽取100名学生；
（2）求出扇形统计图中“C”所对扇形的圆心角的度数，并将条形统计图补充完整；
（3）若该中学共有学生3000人，估计有多少学生在上下学交通方式中选择坐公交车？

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．

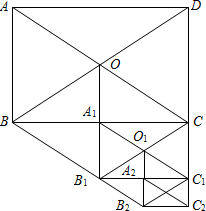如图所示，在矩形ABCD中，AB=12，AC=20，两条对角线相交于点O．以OB、OC为邻边作第1个平行四边形OBB₁C，对角线相交于点A₁，再以A₁B₁、A₁C为邻边作第2个平行四边形A₁B₁C₁C，对角线相交于点O₁；再以O₁B₁、O₁C₁为邻边作第3个平行四边形O₁B₁B₂C₁…依此类推．则第6个平行四边形的面积为（　　）

A．

B．

3.75

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．如图，已知抛物线y=ax²+bx+c（a≠0）经过A（-1，0），B（3，0），C（0，-3）三点，直线l是抛物线的对称轴．
（1）求抛物线的函数关系式；
（2）点M是直线l上的动点，且△MAC为等腰三角形，请直接写出所有符合条件的点M的坐标；
（3）将抛物线向右平移h（h＞0）个单位，所得新抛物线与x轴交于点A₁、B₁，与原抛物线的交点为P，连结PA₁、PB₁，当△PA₁B₁的面积为2时，求此时h的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．计算
（1）101×99
（2）（2a-b）（2a+b）-（2a-b）²．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

解不等式组$\left\{\begin{array}{l}{3（x+1）＜2x+3}\\{\frac{x-1}{3}≤\frac{2}{x}}\end{array}\right.$，并在数轴上表示它们的解集．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．若a、b满足|a-2|+$\sqrt{b+1}$=0，求代数式$\frac{{b}^{3}}{{a}^{2}}$的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．如图1，菱形ABCD中，AB=10，连接BD，tan∠ABD=$\frac{1}{2}$，若P是射线BC上的一个动点（点P不与点B重合），连接AP，与对角线相交于点E，连接EC．
（1）求证：AE=CE；
（2）当点P在线段BC上时，设BP=x，S_△EPC=y，求y关于x的函数解析式，并写出x的取值范围；
（3）当点P在线段BC的延长线上时，若△EPC是直角三角形，求线段BP的长．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学