
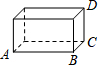
 如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )
如图:长方体的长AB=4厘米、宽BC=2厘米、高CD=3厘米.一只蚂蚁想从A点沿表面爬到D点,则最短距离是( )| A. | 3$\sqrt{5}$ | B. | $\sqrt{41}$ | C. | $\sqrt{29}$ | D. | 5 |
分析 将长方体展开,可分三种情况,求出其值最小者,即为最短路程.
解答 解:展开图有3种情形如图,
在图1中AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
在图2中AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$,
在图3中AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{{7}^{2}+{2}^{2}}$=$\sqrt{53}$,
∵$\sqrt{41}$<3$\sqrt{5}$<$\sqrt{53}$,
∴蚂蚁爬过的最短路程为 $\sqrt{41}$.
故选B.
点评 此题依据“两点之间,线段最短”,考查了长方体的侧面展开图,解答时利用勾股定理进行分类讨论是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为$\frac{64}{27}\sqrt{10}$.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为$\frac{64}{27}\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
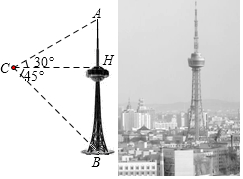 吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)
吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注:$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com