
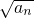 =
=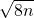 =2
=2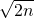 ,所以当n分别取2、8、18、32时得到一列数中从小到大排列的前4个“完全平方数”.
,所以当n分别取2、8、18、32时得到一列数中从小到大排列的前4个“完全平方数”.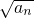 =
=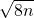 =2
=2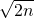 ,根据该式依次列出所需的完全平方数即可.
,根据该式依次列出所需的完全平方数即可.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届海南省八年级(上)期中数学试卷 题型:解答题
设a1=32-12,a2=52-32,…,an=(2n+1)2-(2n-1)2(n为大于0的自然数)
1.探究an是否为8的倍数,并用文字表述出你所获得的结论;
2.若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”,例如:1,4,9,16,…,是“完全平方数”. 试写出a1,a2,a3,…,an,这一列数中从小到大排列的前4个“完全平方数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com