
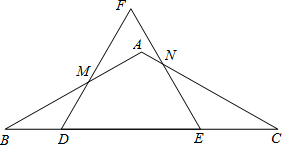
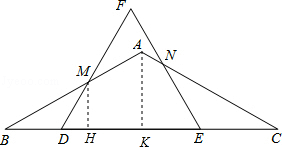
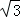 时,以M为圆心,以MF为半径的圆与BC相切
时,以M为圆心,以MF为半径的圆与BC相切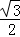 (x﹣2)2+
(x﹣2)2+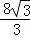 (0≤x≤4)
(0≤x≤4)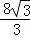 .
. =
=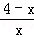 =
= ,
,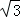 ,
,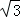 时,以M为圆心,以MF为半径的圆与BC相切;
时,以M为圆心,以MF为半径的圆与BC相切;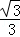 =
=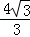 ,
, =
=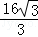 ,
,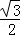 x,
x,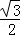 x=
x=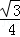 x2,
x2,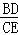 )2=
)2=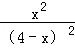 ,
, (4﹣x)2,
(4﹣x)2,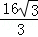 ﹣
﹣ x2﹣
x2﹣ (4﹣x)2=﹣
(4﹣x)2=﹣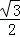 x2+2
x2+2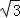 x+
x+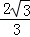 =﹣
=﹣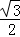 (x﹣2)2+
(x﹣2)2+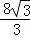 (0≤x≤4),
(0≤x≤4),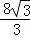 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:单选题
| A.cos600<sin450<tan450 | B.sin450<cos600<tan450 |
| C.cos600<tan450<sin450 | D.tan450<cos600<sin450 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.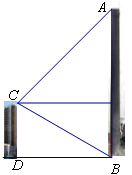
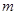 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
远的一棵大树是否被歪倒的烟囱砸着?请说明理由. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
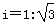 ,AB=10米,AE=15米,求这块宣传牌CD的高度.
,AB=10米,AE=15米,求这块宣传牌CD的高度.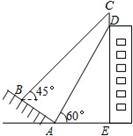
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com