
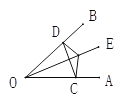
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
【答案】见解析
【解析】
试题(1)根据角平分线性质可证ED=EC,从而可知△CDE为等腰三角形,可证∠ECD=∠EDC;
(2)由OE平分∠AOB,EC⊥OA,ED⊥OB,OE=OE,可证△OED≌△OEC,可得OC=OD;
(3)根据ED=EC,OC=OD,可证OE是线段CD的垂直平分线.
试题解析:证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴ED=EC,即△CDE为等腰三角形,∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,∴△OED≌△OEC(AAS),∴OC=OD;
(3)∵OC=OD,且DE=EC,∴OE是线段CD的垂直平分线.


科目:初中数学 来源: 题型:
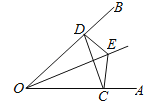
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D,在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是______。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(6x-1)2-25=0; (2)(3x-2)2=x2;
(3)x2+![]() =
=![]() x; (4)(x+1)(x-1)+2(x+3)=8.
x; (4)(x+1)(x-1)+2(x+3)=8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CE⊥AB,垂足为点E,DF⊥AB,垂足为点F,AF=BE,AC=BD,则下列结论:①Rt△AEC≌Rt△BFD;②∠C+∠B=90°;③AC∥BD;④∠A=∠D.
其中正确的结论为____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)求直线l2的函数解析式;
(2)求△ADC的面积;
(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:△NDE≌△MAE;
(2)求证:四边形AMDN是平行四边形;
(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com