
【题目】问题情境:如图1,![]() ,
,![]() ,
,![]() .求
.求 ![]() 度数.
度数.
小明的思路是:如图2,过 ![]() 作
作 ![]() ,通过平行线性质,可得
,通过平行线性质,可得 ![]() .
.

问题迁移:
(1)如图3,![]() ,点
,点 ![]() 在射线
在射线 ![]() 上运动,当点
上运动,当点 ![]() 在
在 ![]() 、
、 ![]() 两点之间运动时,
两点之间运动时,![]() ,
,![]() .
.![]() 、
、 ![]() 、
、 ![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点 ![]() 在
在 ![]() 、
、 ![]() 两点外侧运动时(点
两点外侧运动时(点 ![]() 与点
与点 ![]() 、
、 ![]() 、
、 ![]() 三点不重合),请你直接写出
三点不重合),请你直接写出 ![]() 、
、 ![]() 、
、 ![]() 间的数量关系.
间的数量关系.
【答案】(1)∠CPD=∠α+∠β,理由见解析;(2)①当点P在A、M两点之间时,∠CPD=∠β∠α;②当点P在B、O两点之间时,∠CPD=∠α∠β
【解析】
(1)过点P作PE∥AD交CD于点E,根据题意得出AD∥PE∥BC,从而利用平行线性质可知![]() =∠DPE,
=∠DPE,![]() =∠CPE,据此进一步证明即可;
=∠CPE,据此进一步证明即可;
(2)根据题意分当点P在A、M两点之间时以及当点P在B、O两点之间时两种情况逐一分析讨论即可.
(1)∠CPD=![]() ,理由如下:
,理由如下:
如图3,过点P作PE∥AD交CD于点E,
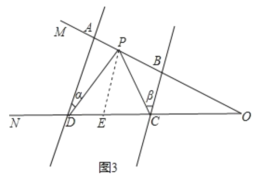
∵AD∥BC,PE∥AD,
∴AD∥PE∥BC,
∴![]() =∠DPE,
=∠DPE,![]() =∠CPE,
=∠CPE,
∴∠CPD=∠DPE+∠CPE=![]() ;
;
(2)①当点P在A、M两点之间时,∠CPD=![]() ,理由如下:
,理由如下:
如图4,过点P作PE∥AD交CD于点E,
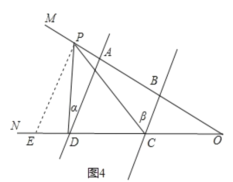
∵AD∥BC,PE∥AD,
∴AD∥PE∥BC,
∴![]() =∠EPD,
=∠EPD,![]() =∠CPE,
=∠CPE,
∴∠CPD=∠CPE∠EPD=![]() ;
;
②当点P在B、O两点之间时,∠CPD=![]() ,理由如下:
,理由如下:
如图5,过点P作PE∥AD交CD于点E,
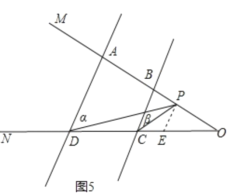
∵AD∥BC,PE∥AD,
∴AD∥PE∥BC,
∴![]() =∠DPE,
=∠DPE,![]() =∠CPE,
=∠CPE,
∴∠CPD=∠DPE∠CPE=![]() ,
,
综上所述,当点P在A、M两点之间时,∠CPD=∠β∠α;当点P在B、O两点之间时,∠CPD=∠α∠β.


科目:初中数学 来源: 题型:
【题目】已知如图,圆锥的母线长6cm,底面半径是3cm,在B处有一只蚂蚁,在AC中点P处有一颗米粒,蚂蚁从B爬到P处的最短距离是( )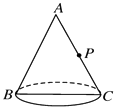
A.3 ![]() cm
cm
B.3 ![]() cm
cm
C.9cm
D.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC中∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠DAC=22.5°,其中正确的是( )

A. ①②④B. ③④⑤C. ①③④D. ①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.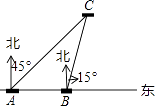
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )
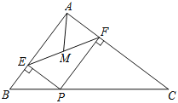
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,先填好下表,再写出总运费y关于x的函数关系式;

(2)若要求总运费不超过900元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,点M为直线AB,CD所确定的平面内的一点,若∠A105,∠M108,请直接写出∠C的度数 ;
(2)如图2,AB∥CD,点P为直线AB,CD所确定的平面内的一点,点E在直线CD上,AN平分∠PAB,射线AN的反向延长线交∠PCE的平分线于M,若∠P30,求∠AMC的度数;
(3)如图3,点P与直线AB,CD在同一平面内,AN平分∠PAB,射线AN的反向延长线交∠PCD的平分线于M,若AMC180![]() P,求证:AB∥CD.
P,求证:AB∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
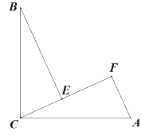
【题目】如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0<∠ACF<45°.
(1)求证:△BEC≌△CEA;
(2)若AF=5,EF=8,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com