
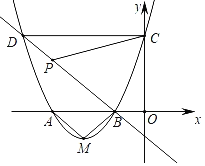
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy£½£Øx+2£©2+mÓėxÖį½»ÓŚA£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£®µćDŌŚÅ×ĪļĻßÉĻ£¬ĒŅÓėµćC¹ŲÓŚÅ×ĪļĻߵĶŌ³ĘÖį¶Ō³Ę£¬Å×ĪļĻߵĶ„µćĪŖM£¬µćBµÄ×ų±źĪŖ£Ø©1£¬0£©£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½¼°A£¬C£¬DµÄ×ų±ź£»
£Ø2£©ÅŠ¶Ļ”÷ABMµÄŠĪד£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£»
£Ø3£©ČōµćPŹĒÖ±ĻßBDÉĻŅ»øö¶Æµć£¬ŹĒ·ń“ęŌŚŅŌP£¬C£¬DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABDĻąĖĘ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ
”¾“š°ø”æ£Ø1£©£»Å×ĪļĻߵĽāĪöŹ½ĪŖy£½£Øx+2£©2©1£»A£Ø©3£¬0£©£»C£Ø0£¬3£©£»D£Ø©4£¬3£©£»£Ø2£©”÷ABMŹĒµČŃüÖ±½ĒČż½ĒŠĪ£»¼ū½āĪö£»£Ø3£©“ęŌŚ£¬ĄķÓɼū½āĪö£»
”¾½āĪö”æ
£Ø1£©°ŃB£Ø©1£¬0£©“śČėÅ×ĪļĻß½āĪöŹ½æÉĒó³öÅ×ĪļĻߵĽāĪöŹ½£¬·Ö±šĮīx=0ŗĶy=0æÉĒóµĆA£¬CµÄ×ų±ź£¬ĄūÓĆÅ×ĪļĻߏĒÖį¶Ō³ĘµÄŠŌÖŹæÉĒóµĆDµÄ×ų±ź£»
£Ø2£©×÷MN”ĶxÖį£¬ĄūÓĆÅ×ĪļĻߏĒÖį¶Ō³ĘµÄŠŌÖŹŅŌ¼°ĢŲŹā½ĒµÄČż½ĒŗÆŹżæÉĒóµĆ”ĻMAN£½”ĻMBN£½45”ć£¬“Ó¶ųµĆµ½”÷ABMŹĒµČŃüÖ±½ĒČż½ĒŠĪ£»
£Ø3£©ŠčŅŖ·ÖĄąĢÖĀŪ£ŗ”÷ABD”×”÷PDC”¢”÷ABD”×”÷CDP£¬øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒóµĆ![]() µÄ³¤¶Č£¬Č»ŗóæÉĒóµĆµć
µÄ³¤¶Č£¬Č»ŗóæÉĒóµĆµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
½ā£ŗ£Ø1£©°ŃB£Ø©1£¬0£©“śČėÅ×ĪļĻß½āĪöŹ½µĆ£¬
£Ø©1+2£©2+m£½0£¬
½āµĆm£½©1£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½£Øx+2£©2©1£¬
µ±y£½0Ź±£¬£Øx+2£©2©1£½0£¬½āµĆx1£½©1£¬x2£½©3£¬
”ąA£Ø©3£¬0£©£®
µ±x£½0Ź±£¬y£½£Øx+2£©2©1£½3£¬
”ąC£Ø0£¬3£©
”ßÅ×ĪļĻ߶Ō³ĘÖįŹĒÖ±Ļßx£½©2£¬C£¬DĮ½µć¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖį¶Ō³Ę£¬
”ąD£Ø©4£¬3£©£»
£Ø2£©”÷ABMŹĒµČŃüÖ±½ĒČż½ĒŠĪ£»
Ö¤Ć÷£ŗ”ßÅ×ĪļĻßy£½£Øx+2£©2©1µÄ¶„µćŹĒM£¬
”ąM£Ø©2£¬©1£©£¬
×÷MN”ĶxÖįÓŚN£¬ŌņN£Ø©2£¬0£©£®
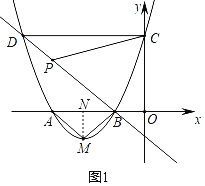
”ąAN£½BN£½MN£½1£¬
”ąAM£½BM£¬
tan”ĻMAN£½tan”ĻMBN£½1£¬
”ą”ĻMAN£½”ĻMBN£½45”ć£¬
”ą”ĻAMB£½180”ć©”ĻMAN©”ĻMBN£½90”ć£¬
”ą”÷ABMŹĒµČŃüÖ±½ĒČż½ĒŠĪ£»
£Ø3£©“ęŌŚ£¬ĄķÓÉ£ŗ
¢Łµ±”÷ABD”×”÷PDCŹ±£¬
![]() £¬¼“£ŗ
£¬¼“£ŗ![]() £¬
£¬
ŌņPD£½![]() £¬
£¬
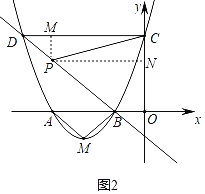
¹żµćP·Ö±š×÷x”¢yÖįµÄ“¹Ļß½»ÓŚµćM”¢N£¬
ŌņPM£½![]() £½DM£¬
£½DM£¬
ŌņµćP£Ø![]() £¬
£¬![]() £©£»
£©£»
¢Śµ±”÷ABD”×”÷CDPŹ±£¬
Ķ¬ĄķæÉµĆ£ŗµćP£Ø2£¬©3£©
×ŪÉĻ£¬µćP£Ø![]() £¬
£¬![]() £©»ņP2£Ø2£¬©3£©
£©»ņP2£Ø2£¬©3£©


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
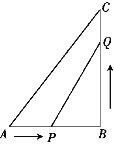
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ,”ĻB=90”ć,AB=5 cm,BC=7 cm£¬µćP“ÓµćAæŖŹ¼ŃŲAB±ßĻņµćBŅŌ1 cm/sµÄĖŁ¶ČŅʶÆ,Ķ¬Ź±µćQ“ÓµćBæŖŹ¼ŃŲBCĻņµćCŅŌ2cm/sµÄĖŁ¶ČŅʶÆ.µ±Ņ»øöµćµ½“ļÖÕµćŹ±ĮķŅ»µćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ,ŌĖ¶ÆŹ±¼äĪŖxĆė(x>0).
(1)Ēó¼øĆėŗó£¬PQµÄ³¤¶ČµČÓŚ5 cm.
(2)ŌĖ¶Æ¹ż³ĢÖŠ£¬”÷PQBµÄĆ껿ÄÜ·ńµČÓŚ8 cm2?²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«”÷ABCČʵćCĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½”÷EDC£®ČōµćA£¬D£¬EŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬”ĻACB=20”ć£¬Ōņ”ĻADCµÄ¶ČŹżŹĒ![]() ””””
””””![]()

A. 55”ć B. 60”ć C. 65”ć D. 70”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼Ņ»ÕÅČż½ĒŠĪÖ½Ę¬ABC£¬±ßAB³¤ĪŖ10cm£¬AB±ßÉĻµÄøßĪŖ15cm£¬ŌŚČż½ĒŠĪÄŚ“Ó×óµ½ÓŅµž·Å±ß³¤ĪŖ2µÄÕż·½ŠĪŠ”Ö½Ę¬£¬µŚŅ»“ĪŠ”Ö½Ę¬µÄŅ»Ģõ±ß¶¼ŌŚABÉĻ£¬ŅĄ“ĪÕāŃłĶłÉĻµž·ÅÉĻČ„£¬Ōņ×ī¶ąÄܵž·ÅµÄÕż·½ŠĪµÄøöŹżŹĒ( ).
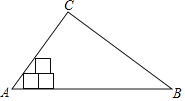
A. 12B. 13C. 14D. 15
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB£½90”ć£¬”ĻBAC£½60”ć£¬AB£½6£¬½«”÷ABCČʵćAÄꏱÕė·½ĻņŠż×Ŗ60”ćµĆµ½”÷AB”äC”䣬ĒóĻ߶ĪB”äCµÄ³¤£®
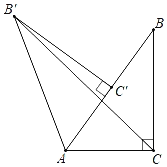
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅ×ĪļĻßy=x2-(m+1)x+mÓėyÖį½»ÓŚ(0£¬-3)µć.
(1)Ēó³ömµÄÖµŗĶÅ×ĪļĻßÓėxÖįµÄ½»µć£»
(2)xČ”Ź²Ć“ÖµŹ±£¬y>0.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖijÖÖÉĢĘ·µÄ½ų¼ŪĪŖĆ漞30ŌŖøĆÉĢĘ·ŌŚµŚxĢģµÄŹŪ¼ŪŹĒy1£Øµ„Ī»£ŗŌŖ/¼ž£©£¬ĻśĮæŹĒy2£Øµ„Ī»£ŗ¼ž£©£¬ĒŅĀś×ć¹ŲĻµŹ½![]() £¬y2£½200©2x£¬ÉčĆæĢģĻśŹŪøĆÉĢĘ·µÄĄūČóĪŖwŌŖ£®
£¬y2£½200©2x£¬ÉčĆæĢģĻśŹŪøĆÉĢĘ·µÄĄūČóĪŖwŌŖ£®
£Ø1£©Š“³öwÓėxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ĻśŹŪøĆÉĢĘ·µŚ¼øĢģŹ±£¬µ±ĢģĻśŹŪĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
£Ø3£©øĆÉĢĘ·ĻśŹŪ¹ż³ĢÖŠ£¬¹²ÓŠ¶ąÉŁĢģČÕĻśŹŪĄūČó²»µĶÓŚ4800ŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
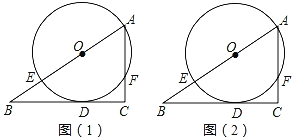
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćEŌŚÖ±½ĒČż½ĒŠĪABCµÄŠ±±ßABÉĻ£¬ŅŌAEĪŖÖ±¾¶µÄ”ŃOÓėÖ±½Ē±ßBCĻąĒŠÓŚµćD£®
£Ø1£©Ēė½öÓĆĪŽæĢ¶ČµÄÖ±³ßŌŚĶ¼1ÖŠ×÷³ö”ĻBACµÄĘ½·ÖĻߣ»
£Ø2£©Ēė½öÓĆĪŽæĢ¶ČµÄÖ±³ßŌŚĶ¼2ÖŠµÄĻ߶ĪBCÉĻČ”Ņ»øöµćP£¬Ź¹CP£½EF£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
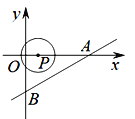
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() ½»xÖįÓŚµćA£¬½»yÖįÓŚµćB£¬µćPŹĒxÖįÉĻŅ»¶Æµć£¬ŅŌµćPĪŖŌ²ŠÄ£¬ŅŌ1øöµ„Ī»³¤¶ČĪŖ°ė¾¶×÷”ŃP£¬µ±”ŃPÓėÖ±ĻßABĻąĒŠŹ±£¬µćPµÄ×ų±źŹĒ______________.
½»xÖįÓŚµćA£¬½»yÖįÓŚµćB£¬µćPŹĒxÖįÉĻŅ»¶Æµć£¬ŅŌµćPĪŖŌ²ŠÄ£¬ŅŌ1øöµ„Ī»³¤¶ČĪŖ°ė¾¶×÷”ŃP£¬µ±”ŃPÓėÖ±ĻßABĻąĒŠŹ±£¬µćPµÄ×ų±źŹĒ______________.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com