
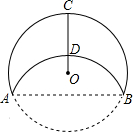
 如图,将半径为12的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )
如图,将半径为12的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )| A. | 3$\sqrt{15}$ | B. | 4$\sqrt{15}$ | C. | 6$\sqrt{15}$ | D. | 12 |
科目:初中数学 来源: 题型:解答题
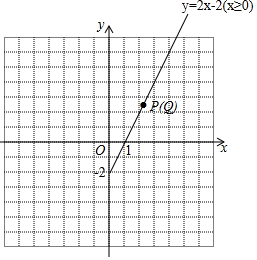 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若$y'=\left\{\begin{array}{l}y(x≥0)\\-y(x<0)\end{array}\right.$,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).
在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若$y'=\left\{\begin{array}{l}y(x≥0)\\-y(x<0)\end{array}\right.$,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
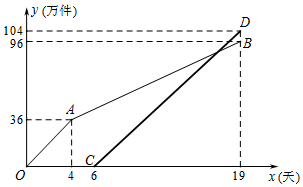 爱贝玩具厂开发了一款新型益智玩具,一期计划生产200万件,预计20天后投入市场.该厂有甲、乙、丙三条生产线,由于丙生产线在技术创新升级中,则由甲、乙两条生产线先开始生产加工玩具.甲、乙两条生产线一起生产加工玩具4天后,乙生产线发生故障停止生产,只剩甲生产线单独加工玩具.为了能在规定时间完成任务,丙生产线加快了技术升级,6天后也投入生产.由于丙生产线技术升级后提高了效率,所以提前一天完成加工任务.已知甲、乙两条生产线生产玩具总量y1(万件)与时间x(天)的关系如图折线段OAB所示,丙生产线生产玩具总量y2(万件)与时间x(天)的关系如图线段CD所示.
爱贝玩具厂开发了一款新型益智玩具,一期计划生产200万件,预计20天后投入市场.该厂有甲、乙、丙三条生产线,由于丙生产线在技术创新升级中,则由甲、乙两条生产线先开始生产加工玩具.甲、乙两条生产线一起生产加工玩具4天后,乙生产线发生故障停止生产,只剩甲生产线单独加工玩具.为了能在规定时间完成任务,丙生产线加快了技术升级,6天后也投入生产.由于丙生产线技术升级后提高了效率,所以提前一天完成加工任务.已知甲、乙两条生产线生产玩具总量y1(万件)与时间x(天)的关系如图折线段OAB所示,丙生产线生产玩具总量y2(万件)与时间x(天)的关系如图线段CD所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3a+b)(3b-a) | B. | ($\frac{1}{3}a$+1)(-$\frac{1}{3}a$-1) | C. | (a-b)(-a+b) | D. | (-a-b)(-a+b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
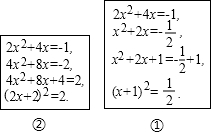 在解方程2x2+4x+1=0时,对方程进行配方,文本框①中是嘉嘉作的,文本框②中是琪琪作的,对于两人的做法,说法正确的是( )
在解方程2x2+4x+1=0时,对方程进行配方,文本框①中是嘉嘉作的,文本框②中是琪琪作的,对于两人的做法,说法正确的是( )| A. | 两人都正确 | B. | 嘉嘉正确,琪琪不正确 | ||
| C. | 嘉嘉不正确,琪琪正确 | D. | 两人都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
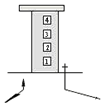 一幢4层楼房只有一个房间亮着灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的房间是( )
一幢4层楼房只有一个房间亮着灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的房间是( )| A. | 1号房间 | B. | 2号房间 | C. | 3号房间 | D. | 4号房间 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com