
 如图,长5m的梯子MN以倾斜角62°架在墙上,若梯子的顶端M下滑一定距离后,底端N向左滑动0.65m,顶端M下滑了多长距离(精确到0.01m)?
如图,长5m的梯子MN以倾斜角62°架在墙上,若梯子的顶端M下滑一定距离后,底端N向左滑动0.65m,顶端M下滑了多长距离(精确到0.01m)? 分析 首先在地面、梯子以及墙三者形成的直角三角形中,已知一个锐角和斜边,求对边,依据正弦函数即可求解,再求出PC,用勾股定理求出PA即可.
解答 解:如图,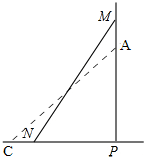
在Rt△MPN中,∠PNM=62°,MN=5,
∴PM=MNsin∠PNM=5sin62°≈5×0.88=4.4,
PN=MNcos∠PNM=5cos62°≈5×0.47=2.35,
∵梯子的顶端M下滑一定距离后,底端N向左滑动0.65m,
∴PC=PN+CN=2.35+0.65=3,
根据勾股定理得,PA=$\sqrt{A{C}^{2}-P{C}^{2}}$=4,
∴MA=PM-PA=4.4-4=0.4,
∴顶端M下滑了0.4m.
点评 本题主要考查了正弦函数的定义,勾股定理,把实际问题抽象成数学问题是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,两同心圆中,大圆的弦AB交小圆于C、D两点,点O到AB的距离等于CD的一半,且AC=CD.则大小圆的半径之比为( )
如图,两同心圆中,大圆的弦AB交小圆于C、D两点,点O到AB的距离等于CD的一半,且AC=CD.则大小圆的半径之比为( )| A. | $\sqrt{5}$:1 | B. | 2:$\sqrt{10}$ | C. | 10:$\sqrt{2}$ | D. | 3:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 -3x=x2-5x+1,若x=$\sqrt{6}+1$,则所捂二次三项式的值为6.
-3x=x2-5x+1,若x=$\sqrt{6}+1$,则所捂二次三项式的值为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买量 | 购买量 | |
| A型车 | 4 | 5 |
| B型车 | 5 | 4 |
| 总价 | 128万元 | 124万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com