练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    运算： ， ，

    ， ，

    ， ．

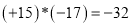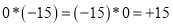    （）请你认真思考上述运算，归纳*运算的法则：两数进行*运算时，__________．

    特别地， 和任何数进行*运算，或任何数和进行*运算，__________．

    （）计算： __________．

    （）是否存在有理数、，使得，若存在，求出、的值，若不存在，说明理由．

    （）同号两数，取正号，并把绝对值相加，等于这个数的绝对值（）23（） 【解析】试题分析：（1）根据所给算式，总结规律即可； （2）根据（1）的规律进行计算即可； （3）根据（1）的规律进行计算求解. 试题解析：（）同号两数，取正号，并把绝对值相加，等于这个数的绝对值． （） ． （）由定义可知， ∵， ∴， ∴．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南省双柏县2017-2018学年八年级上期期末数学试卷 题型：解答题

    如图，已知DE∥BC，BE是∠ABC的平分线，∠C=70°，∠ABC=50°．求∠DEB和∠BEC的度数．

    ∠DEB=25°，∠BEC=85°． 【解析】试题分析：根据平行线的性质和三角形的内角和定理进行解答． 试题解析：【解析】 ∵ BE是∠ABC的平分线，∠ABC=50°，∴∠1=∠2=25°．∵ DE∥BC，∴∠DEB =∠2=25°． 在△BEC中，∠C=70°，∴∠BEC =180°-∠C-∠2=180°-70°-25°=85°．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，在平面直角坐标系中，已知点A（-3，6），B（-9，-3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（　　）

    A. （-1，2） B. （-9，18） C. （-9，18）或（9，-18） D. （-1，2）或（1，-2）

    D 【解析】试题分析：根据位似图形的性质可得：点A′的坐标为(-3×，6×)或[-3×(-)，6×(-)]，即点A′的坐标为(-1,2)或(1，-2).

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    在Rt△ABC中，∠C=90°，若sinA=，则cosB的值是____________ ．

    【解析】试题分析：如图： 在Rt△ABC中，∠C=90°．因为sinA=，不妨设BC=3k，AB=5k，cosB=

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：单选题

    如图，在⊙O中， ，∠AOB=40°，则∠ADC的度数是（　　）

    A. 40° B. 30° C. 20° D. 15°

    C 【解析】连接CO，如图： ∵在⊙O中, ， ∴∠AOC=∠AOB， ∵∠AOB=40°， ∴∠AOC=40°， ∴∠ADC=∠AOC=20°， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    解方程：

    （）．

    （）．

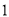    （1）（2）x=3 【解析】试题分析：先去括号，然后移项合并，最后化系数为1即可得出方程的解． 试题解析：（） ∴． （） ∴．

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    如图，从边长为的正方形纸片中剪去一个边长为的正方形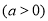，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的周长为__________ ．

    【解析】试题解析：如图 可知（长宽） ． 故答案为：4a+16.

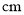    查看答案和解析>>

    科目：初中数学 来源：天津市2018届九年级（上）第四周周清数学试卷 题型：填空题

    抛物线y=2x2﹣bx+3的对称轴是直线x=1，则b的值为 ．

    4. 【解析】试题考查知识点：抛物线y＝ax2+bx＋c(a≠0)的对称轴是直线 思路分析：直接套用对称轴解析式即可得到关于系数b的方程 具体解答过程： ∵抛物线y＝ax2+bx＋c(a≠0)的对称轴是直线，抛物线y＝2x2－bx＋3的对称轴是直线x＝1 ∴ 解之得：b=4

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    解方程：（1）；（2）.

    （1）x=-1；(2)x=-15. 【解析】试题分析：两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解． 试题解析：（1） 去分母得：3x=x-2， 解得：x=-1， 经检验：x=-1是原方程的根. （2） 去分母得：（x+3）2-4(x-3)=(x-3)(x+3) 解得：x=-15 经检验：x=-15是原...

    查看答案和解析>>

    同步练习册答案