
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,切线
,切线![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
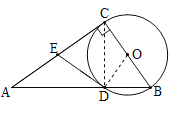
(1)连接OD.只要证明∠A+∠B=90°,∠ADE+∠B=90°即可解决问题;
(2)首先证明AC=2DE=20.在Rt△ADC中,由勾股定理得到DC的长,设BD=x.在Rt△BDC中,BC2=x2+122.在Rt△ABC中,BC2=(x+16)2﹣202,可得x2+122=(x+16)2﹣202,解方程即可解决问题.
(1)连接OD.
∵DE是切线,∴∠ODE=90°,∴∠ADE+∠BDO=90°.
∵∠ACB=90°,∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO,∴∠ADE=∠A.
(2)连接CD.
∵∠ADE=∠A,∴AE=DE.
∵BC是⊙O的直径,∠ACB=90°,
∴EC是⊙O的切线,∴ED=EC,∴AE=EC.
∵DE=10,∴AC=2DE=20,
在Rt△ADC中,DC![]() 12,
12,
设BD=x.在Rt△BDC中,BC2=x2+122.
在Rt△ABC中,BC2=(x+16)2﹣202,
∴x2+122=(x+16)2﹣202,
解得x=9,∴BC![]() 15.
15.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
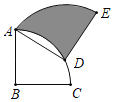
【题目】如图,扇形ABC的圆心角为90°,半径为6,将扇形ABC绕A点逆时针旋转得到扇形ADE,点B、C的对应点分别为点D、E,若点D刚好落在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
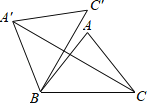
【题目】如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A'BC’,连接A'C,则A'C的长为( )
A. 6B. 4+2![]() C. 4+3
C. 4+3![]() D. 2+3
D. 2+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
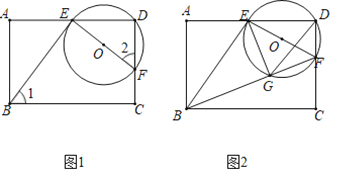
【题目】如图1,在矩形ABCD中,点E以lcm/s的速度从点A向点D运动,运动时间为t(s),连结BE,过点E作EF⊥BE,交CD于F,以EF为直径作⊙O.
(1)求证:∠1=∠2;
(2)如图2,连结BF,交⊙O于点G,并连结EG.已知AB=4,AD=6.
①用含t的代数式表示DF的长
②连结DG,若△EGD是以EG为腰的等腰三角形,求t的值;
(3)连结OC,当tan∠BFC=3时,恰有OC∥EG,请直接写出tan∠ABE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
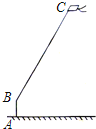
【题目】周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
 ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级组织了“我和我的祖国”演讲比赛,甲、乙两队各有10人参加本次比赛,成绩如下(10分制)
甲 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
乙 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
(1)甲队成绩的众数是 分,乙队成绩的中位数是 分.
(2)计算乙队成绩的平均数和方差.
(3)已知甲队成绩的方差是1分2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com