
【题目】如图(1),在等边三角形![]() 中,
中,![]() 是
是![]() 边上的动点,以
边上的动点,以![]() 为一边,向上作等边三角形
为一边,向上作等边三角形![]() ,连接
,连接![]() .
.
(1)![]() 和
和![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)试说明:![]() ;
;
(3)如图(2),将动点![]() 运动到边
运动到边![]() 的延长线上,所作三角形
的延长线上,所作三角形![]() 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有![]() ?请说明理由.
?请说明理由.

【答案】(1)![]() 和
和![]() 全等,理由见解析;(2)过程见解析;(3)仍有
全等,理由见解析;(2)过程见解析;(3)仍有![]() ,理由见解析.
,理由见解析.
【解析】
(1)要证两个三角形全等,已知的条件有:AC=BC,CE=CD,且∠BCD和∠ACE都是60°减去一个∠ACD,即可证明两个三角形全等;
(2)根据△DBC≌△EAC可得∠EAC=∠B=60°,又∠ACB=60°,所以∠EAC=∠ACB,即可得出结论;
(3)结合(1)(2)问的思路证明即可得出答案.
解:(1)![]() 和
和![]() 全等
全等
证明:∵△ABC和△DEC均为等边三角形
∴∠ACB=∠ECD=60°,BC=AC,CD=CE
又∠ACB=∠BCD+∠ACD
∠ECD=∠ECA+∠ACD
∴∠BCD=∠ECA
在△DBC和△EAC中
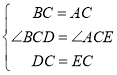
∴△DBC≌△EAC(SAS)
(2)∵△DBC≌△EAC
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC
(3)仍有AE∥BC
理由:∵△ABC和△DEC均为等边三角形
∴∠ACB=∠ECD=60°,BC=AC,CD=CE
∴∠BCA+∠ACD=∠ACD+∠DCE
∴∠BCD=∠ACE
在△DBC和△EAC中
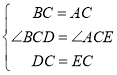
∴△DBC≌△EAC(SAS)
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC


科目:初中数学 来源: 题型:
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
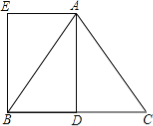
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1 500t,则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,甲地到乙地的路程为450千米,一辆大货车从甲地前往乙地运送物资,行驶1小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过半小时修好大货年后以原速原路返甲地,小汽车在返程途中当走到一半路程时发现有重要物品落在大货车上,于是立即掉头以原速追赶大货车,追上大货车取下物品(取物品时间忽略不计)后以原速原路返回甲地,大货车修好后以原速前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则当小汽车第二次追上大货车时,大货车距离乙地_____千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
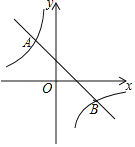
【题目】如图,一次函数y1=kx+2图象与反比例函数y2=![]() 图象相交于A,B两点,已知点B的坐标为(3,﹣1).
图象相交于A,B两点,已知点B的坐标为(3,﹣1).
(1)求一次函数和反比例函数的解析式;
(2)请直接写出不等式kx﹣![]() ≤﹣2的解集;
≤﹣2的解集;
(3)点C为x轴上一动点,当S△ABC=3时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中的网格由单位正方形构成,![]() 中,
中,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .
.
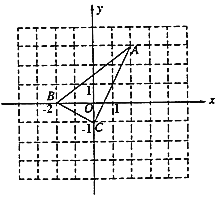
(1)![]() 的长为_______;
的长为_______;
(2)求证:![]() ;
;
(3)若以![]() 、
、![]() 、
、![]() 及点
及点![]() 为顶点的四边形为平行四边形,写出
为顶点的四边形为平行四边形,写出![]() 点在第一象限时的坐标______.
点在第一象限时的坐标______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com