
 ��ͼ����ֱ������ϵ�У���֪��A��0��2������B��-2��0��������B���߶�OA���е�C��ֱ��BC�����߶�BCΪ��������������BCDE��
��ͼ����ֱ������ϵ�У���֪��A��0��2������B��-2��0��������B���߶�OA���е�C��ֱ��BC�����߶�BCΪ��������������BCDE������ ��1������ȫ�������Σ���ȫ�������ζ�Ӧ�߶�֮�����ȹ�ϵ�������D����E�����ꣻ
��2�����ô���ϵ������������ߵĽ���ʽ���ɣ�
��3�����ʷdz����ӣ���С��˼������㣺��Ϊ��s�ı���ʽ����Ҫʶ�������Σ��������ߣ����˶����̣������ε�ƽ�ƣ��ӿ�ʼ���������ܹ���ʱ1.5�룬�ڼ���Ի��ֳ������Σ���0��t��0.5ʱ����Ӧͼ��3��a����0.5��t��1ʱ����Ӧͼ��3��b����1��t��1.5ʱ����Ӧͼ��3��c��ÿ���εı���ʽ��ͬ�������ͼ������˼�����ڵ��˶�ֹͣʱ����E����y�ᣬ��E��-3��2���˶�����E�䣨0��3.5������֪��������������ƽ����3����λ������ƽ����1.5����λ���ɴ˵õ�ƽ��֮��������߽���ʽ����������䶥�����꣮
��� 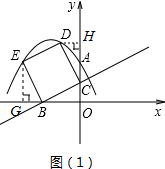 �⣺��1���������֪��OB=2��OC=1��
�⣺��1���������֪��OB=2��OC=1��
��ͼ��1����ʾ����D����DH��y����H����E����EG��x����G��
��֤��CDH�ա�BCO��
��DH=OC=1��CH=OB=2��
��D��-1��3����
ͬ����EBG�ա�BCO��
��BG=OC=1��EG=OB=2��
��E��-3��2����
��D��-1��3����E��-3��2����
�ʴ�Ϊ����-1��3����-3��2����
��2�������߾�����0��2������-1��3������-3��2����
��$\left\{\begin{array}{l}{c=2}\\{a-b+c=3}\\{9a-3b+c=2}\end{array}\right.$?
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$��
��y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2��
��3���ٵ���D�˶���y����ʱ��t=$\frac{1}{2}$��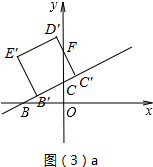
��0��t��$\frac{1}{2}$ʱ����ͼ��3��a��ʾ��
��D��C�佻y���ڵ�F
��tan��BCO=$\frac{OB}{OC}$=2��
�֡ߡ�BCO=��FCC��
��tan��FCC��=2����$\frac{FC��}{CC��}$=2
��CC��=$\sqrt{5}$t��
��FC��=2$\sqrt{5}$t��?
��S��CC��F=$\frac{1}{2}$CC��•FC��=$\frac{1}{2}$t��2$\sqrt{5}$t=5t2
����B�˶�����Cʱ��t=1��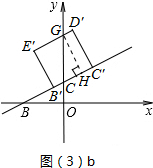
��0.5��t��1ʱ����ͼ��3��b��ʾ��
��D��E�佻y���ڵ�G����G��GH��B��C����H��
��Rt��BOC��BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��
��GH=$\sqrt{5}$����CH=$\frac{1}{2}$GH=$\frac{\sqrt{5}}{2}$��
��CC��=$\sqrt{5}$t��
��HC��=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$��
��GD��=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$��
��S����CC��D��G?=$\frac{1}{2}$��$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$+$\sqrt{5}$t��=5t-$\frac{5}{4}$��
����E�˶���y����ʱ��t=1.5��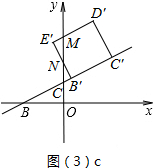
��1��t��15ʱ����ͼ��3��c��ʾ
��D��E�䡢E��B��ֱ�y���ڵ�M��N��
��CC��=$\sqrt{5}$t��B��C��=$\sqrt{5}$��
��CB��=$\sqrt{5}$t-$\sqrt{5}$��?��B��N=2CB��=2$\sqrt{5}$t-2$\sqrt{5}$��
��B��E��=$\sqrt{5}$����E��N=B��E��-B��N=3$\sqrt{5}$-2$\sqrt{5}$t
��E��M=$\frac{1}{2}$E��N=$\frac{1}{2}$��3$\sqrt{5}$-2$\sqrt{5}$t����
��S��MNE��?=$\frac{1}{2}$��3$\sqrt{5}$-2$\sqrt{5}$t��•$\frac{1}{2}$��3$\sqrt{5}$-2$\sqrt{5}$t��=5t2-15t+$\frac{45}{4}$��
��S�����B��C��D��MN?=S������B��C��D��E��?-S��MNE��?=2$\sqrt{5}$��5t2-15t+$\frac{45}{4}$��=-5t2+15t-$\frac{25}{4}$��
����������S��x�ĺ�����ϵʽΪ��
��0��t��0.5ʱ��S=5t2
��0.5��t��1ʱ��S=5t-$\frac{5}{4}$��
��1��t��1.5ʱ��S=-5t2+15t-$\frac{25}{4}$��
�ڵ���E�˶�����E��ʱ���˶�ֹͣ����ͼ��3��d��ʾ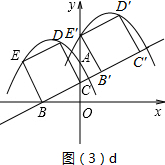 ��
��
�ߡ�CB��E��=��BOC=90�㣬��BCO=��B��CE�䣬
���BOC�ס�E��B��C��
��$\frac{OB}{B��E��}$=$\frac{BC}{E��C}$��
��OB=2��B��E��=BC=$\sqrt{5}$��
��$\frac{2}{\sqrt{5}}=\frac{\sqrt{5}}{E��C}$��
��CE��=2.5��
��OE��=OC+CE��=1+2.5=3.5��
��E�䣨0��3.5����
�ɵ�E��-3��2���˶�����E�䣨0��3.5������֪��������������ƽ����3����λ������ƽ����1.5����λ��
��y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=-$\frac{1}{2}$��x+$\frac{3}{2}$��2+$\frac{25}{8}$��
��ԭ�����߶�������Ϊ��-$\frac{3}{2}$��$\frac{25}{8}$����
���˶�ֹͣʱ�������ߵĶ�������Ϊ��$\frac{3}{2}$��$\frac{37}{8}$����
���� �����Ƿdz����͵Ķ������ۺ��⣬ȫ�濼���˳�����ѧ�������εĶ����Ҫ֪ʶ�㣬���������κ�����ͼ�������ʡ�����ϵ���������ʽ���������뼸�α任��ƽ�ƣ������������ε��ж������ʡ�ȫ�������ε��ж������ʡ������ε����ʵȣ��ѵ����ڵڣ�3���ʣ�ʶ�������κ�������ƽ�ƹ��̵IJ�ͬ���ǹؼ����ڣ���Ϊ�п�ѹ���⣬�����漰�����ڶ࣬���㸴�ӣ�����ѶȺܴԿ����ۺ�����Ҫ��ܸߣ����кܺõ����ֶȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
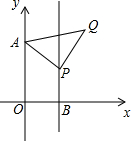 ��ͼ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬A��0��5����B��3��0��������B��ֱ��l��y�ᣬ��P��3��b����ֱ��l�ϵ�һ�����㣬��APΪ����AP�Ҳ�������Rt��APQ����APQ=90�㣬����P��ֱ��l���˶�ʱ����QҲ��ʱ֮�˶����ʣ���b=$\frac{23}{7}$ʱ��AQ+BQ��ֵ��СΪ$\sqrt{130}$��
��ͼ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬A��0��5����B��3��0��������B��ֱ��l��y�ᣬ��P��3��b����ֱ��l�ϵ�һ�����㣬��APΪ����AP�Ҳ�������Rt��APQ����APQ=90�㣬����P��ֱ��l���˶�ʱ����QҲ��ʱ֮�˶����ʣ���b=$\frac{23}{7}$ʱ��AQ+BQ��ֵ��СΪ$\sqrt{130}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{10}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| �꼶 | ���꼶 | ���꼶 | ���꼶 |
| �ϸ����� | 270 | 262 | 254 |
| A�� | ���꼶�ĺϸ������ | B�� | ���꼶��ѧ������Ϊ262�� | ||
| C�� | ���꼶�ĺϸ��ʸ���ȫУ�ĺϸ��� | D�� | ���꼶�ĺϸ��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
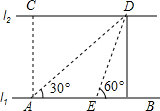 ��ͼ���ӵ�����l1��l2�ƽ�У�A��B��l1�ϵ����㣬C��D��l2�ϵ����㣬ij���ڵ�A����á�CAB=90�㣬��DAB=30�㣬����AB����ǰ��20�����E����E���߶�AB�ϣ�����á�DEB=60�㣬��C��D�����ľ��룮
��ͼ���ӵ�����l1��l2�ƽ�У�A��B��l1�ϵ����㣬C��D��l2�ϵ����㣬ij���ڵ�A����á�CAB=90�㣬��DAB=30�㣬����AB����ǰ��20�����E����E���߶�AB�ϣ�����á�DEB=60�㣬��C��D�����ľ��룮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com