
���壺���һ��y��x�ĺ���ͼ��ƽ�ƺ�����ij������������ͼ���غϣ���ô�����������y��x�ġ�������ƽ�ƺ����������磺 ��ͼ������ƽ��2����λ��������ƽ��1����λ�õ�
��ͼ������ƽ��2����λ��������ƽ��1����λ�õ� ��ͼ����
��ͼ���� ��y��x�ġ�������ƽ�ƺ�������
��y��x�ġ�������ƽ�ƺ�������
��1�������ε����߷ֱ���2cm��3cm���������߷ֱ�����x��cm����y��cm���õ����¾��ε����Ϊ8cm2����y��x�ĺ�������ʽ�����ж���������Ƿ�Ϊ��������ƽ�ƺ�������
��2����ͼ����ƽ��ֱ������ϵ�У���OΪԭ�㣬����OABC�Ķ���A��C������ֱ�Ϊ��9��0������0��3������D��OA���е㣬����OB��CD���ڵ�E����������ƽ�ƺ����� ��ͼ��B��E���㣮�������������ƽ�ƺ������ı���ʽΪ �������������ƽ�ƺ�������ͼ���ʵ��ı任��ijһ��������������ͼ���غϣ���д����������������ı���ʽ��
��ͼ��B��E���㣮�������������ƽ�ƺ������ı���ʽΪ �������������ƽ�ƺ�������ͼ���ʵ��ı任��ijһ��������������ͼ���غϣ���д����������������ı���ʽ��
��3���ڣ�2���������£���֪���߶�BE�е��һ��ֱ��l�������������ƽ�ƺ�����ͼ����P��Q���㣨P��Q���Ҳࣩ����B��E��P��QΪ������ɵ��ı������Ϊ16���������P�����꣮
��1�� ���ǣ���2��
���ǣ���2�� ��
�� ����3����7��5����15��
����3����7��5����15�� ����
����
���������������1�������¾��ε����Ϊ8cm2�����Կ�������������ɵõ�һ������x��y�ķ��̣����ɱ��γɺ�������ʽ�������ж�.
��2����B��D��������� �����з������a��k��ֵ����������ʽ�������.
�����з������a��k��ֵ����������ʽ�������.
��3���ɷ��������������ĶԳ��ԣ��ı���PEQBΪƽ���ı��Σ���P1��x0��y0��������S��OP1E=S�ı���ONMC-S��OCP1-S��MP1E-S��ONE�������з�����⣮
�����������1���ߣ�x+2����y+3��=8��
�� ����ƽ��2����λ��������ƽ��3����λ�õ�
����ƽ��2����λ��������ƽ��3����λ�õ� .
.
�� �ǡ�������ƽ�ƺ�������
�ǡ�������ƽ�ƺ�������
��2����B��D��������� �ã�
�ã� ����ã�
����ã� .
.
������ƽ�ƺ������ı���ʽΪ .
.
�ʱ任��ķ�������������ʽΪ .
.
��3����ͼ������P�ڵ�B���ʱ�����߶�BE���е�ΪF���ɷ������������ĶԳ��ԣ��ı���PEQBΪƽ���ı��Σ�
���ı���PEQB�����Ϊ16����S��PFE=4��
��B��9��3����F��6��2���� ��
�� �ġ�������ƽ�ƺ�������
�ġ�������ƽ�ƺ�������
��S��PFE=S��POE=4����E�������ǣ���3��1��.
��E��x��Ĵ��ߣ���BC��x��ֱ���M��N�㣮
S��OP1E=S�ı���ONMC-S��OCP1-S��MP1E-S��ONE��
��P1��x0��y0����
�� ����
���� �����
����� .
.
��P1��1��3����
���P��������7��5����
����P�ڵ�B�Ҳ�ʱ��ͬ���ɵõ�P������Ϊ��15�� ����
����
������������P��������7��5����15�� ����
����
���㣺1.�����������ۺ��⣻2.�¶��壻3.ƽ�Ƶ����ʣ�4.ת��˼��ͷ���˼���Ӧ�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ,��A�Ƿ���������ͼ���ϵ�һ��,����A�ֱ���x�ᡢy��������, ������ABOC�����Ϊ3,����������������Ĺ�ϵʽ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������������ֽƬPAB��ֱ�Ƕ���P���ڵ������ޣ�����A��B�ֱ����ڷ��������� ͼ�����֧�ϣ���PB��x�ڵ�C��PA��y�ڵ�D��AB�ֱ���x�ᣬy���ཻ�ڵ�E��F����֪B��1��3����
ͼ�����֧�ϣ���PB��x�ڵ�C��PA��y�ڵ�D��AB�ֱ���x�ᣬy���ཻ�ڵ�E��F����֪B��1��3����
��1��k= ��
��2����˵��AE=BF��
��3�����ı���ABCD�����Ϊ ʱ�����P�����꣮
ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��
��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��
��1����һ�κ����������������Ľ���ʽ��
��2������������ͼ�����Ƿ���ڵ�D��ʹ�ı���BCPDΪ���Σ�������ڣ������D�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������OABC�����ڵ�һ�����ڣ���֪A(3��0)����AOB��30�㣬����������y�� ��ͼ��BC��AB�ڵ�D��E��
��ͼ��BC��AB�ڵ�D��E��
(1)����DΪBC���е㣬��֤����EΪAB���е㣻
(2)����A����ֱ��OB�ĶԳƵ�ΪF����̽������F�Ƿ����ڸ�˫�����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ͼ������������ ��ͼ���뷴��������
��ͼ���뷴�������� ��ͼ���ڵ�
��ͼ���ڵ�
��1����ȷ�����������������ͷ����������ı���ʽ��
��2������ͼ��ش��ڵ�һ�����ڣ��� ȡ��ֵʱ��������������ֵ����������������ֵ��
ȡ��ֵʱ��������������ֵ����������������ֵ��
��3��M(m,n)�Ƿ���������ͼ���ϵ�һ����,����0<m<3,��M��ֱ��MB��x�ύy���ڵ�B������A��ֱ��AC��y�ύ�ڵ�C����ֱ��MB�ڵ�D�����ı���OADM�����Ϊ6ʱ�����ж��߶�BM��DM�Ĵ�С��ϵ����˵�����ɣ�
��4��̽����x�����Ƿ���ڵ�P,ʹ��OAP�ǵ��������Σ������ڣ������P�����꣬�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����һ�ֲ�Ʒ�����Ƚ����ϼ��ȴﵽ60 ����ٽ��в�������ò����¶�Ϊy���棩���Ӽ��ȿ�ʼ�����ʱ��Ϊx��min�������˽⣬���ò��ϼ���ʱ���¶�y��ʱ��x��һ�κ�����ϵ��ֹͣ���Ƚ��в���ʱ���¶�y��ʱ��x�ɷ�������ϵ����ͼ������֪�ò����ڲ�������ǰ���¶�Ϊ15 �棬����5���Ӻ��¶ȴﵽ60 �森
��1���ֱ���������ϼ��Ⱥ�ֹͣ���Ƚ��в���ʱ��y��x�ĺ�����ϵʽ��
��2�����ݹ���Ҫ�����ϵ��¶ȵ���15 ��ʱ����ֹͣ��������ô�ӿ�ʼ���ȵ�ֹͣ�������������˶���ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ��� �뷴��������
�뷴��������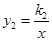 ��ͼ���ڵ�
��ͼ���ڵ� ��
��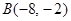 ����
���� �ύ�ڵ�
�ύ�ڵ� ��(1)
��(1) ,
, ��
��
(2)���ݺ���ͼ���֪���� ʱ��
ʱ�� ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
(3)���� ��
�� ���ڵ�
���ڵ� ����
���� �Ƿ����������ڵ�һ����ͼ����һ��,��ֱ��
�Ƿ����������ڵ�һ����ͼ����һ��,��ֱ�� ���߶�
���߶� ���ڵ�
���ڵ� ����
���� ʱ�����
ʱ����� ������.
������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com