设凸四边形ABCD的对角线相交于点O,且AD∥BC,则下面的四个命题:
①已知AB+BC=AD+DC,则ABCD为平行四边形
②已知DC+DO=AO+AB,则ABCD为平行四边形
③已知BC+BO+AO=AD+DO+CO,则ABCD为平行四边形
④已知AD+CO=BC+AO,则ABCD为平行四边形
其中正确命题的序号是________.(可以多选)
①、③、④
分析:①延长AD到F使得DF=DC,延长CB到E使得BE=AB,通过求证四边形AECF是平行四边形,即可推出∠E=∠F,∠EAF=∠ECF,其次根据∠E=∠BAE,∠F=∠DCF,推出∠BAE=∠DCF,即可求出∠BAD=∠BCD,再由∠BCA=∠DAC,求出∠BAC=∠DCA,即可推出AB∥CD,最后由对边分别平行即可推出四边形ABCD为平行四边形,②首先假设命题中的结论成立,根据平行四边形的性质推出AB=CD,OA=OC,根据等式的性质得到等式DC+CO=AO+AB,而不是题设中的DC+DO=AO+AB,由此推出假设不成立,③首先假设四边形ABCD为平行四边形,根据平行四边形的性质推出AD=BC,AB=CD,OA=OC,OB=OD,
根据等式的性质可推出BC+BO+AO=AD+DO+CO,由此可得假设成立,④首先假设四边形ABCD为平行四边形,根据平行四边形的性质推出AD=BC,OA=OC,根据等式的性质可推出AD+CO=BC+AO,由此可得假设成立.
解答:①延长AD到F使得DF=DC,延长CB到E使得BE=AB,
∴∠E=∠BAE,∠F=∠DCF,
∵AB+BC=AD+DC,
即BE+BC=AD+DF,
∴AF=CE,
∵AD∥BC,

∴AF∥CE,∠BCA=∠DAC,
∴四边形AECF是平行四边形,
∴∠E=∠F,∠EAF=∠ECF,
∵∠E=∠BAE,∠F=∠DCF,
∴∠BAE=∠DCF,
∴∠BAD=∠BCD,
∵∠BCA=∠DAC,
∴∠BAC=∠DCA,
∴AB∥CD,
∴四边形ABCD为平行四边形,
∴本项正确,

②假设四边形ABCD是平行四边形,
∴AB=CD,OA=OC,
∴DC+CO=AO+AB,
∵DC+DO=AO+AB,
∴假设不成立,
∴本项错误;
③假设四边形ABCD为平行四边形,

∴AD=BC,AB=CD,OA=OC,OB=OD,
∴BC+BO+AO=AD+DO+CO,
∴假设成立,
∴本项正确,
④假设四边形ABCD为平行四边形,
∴AD=BC,OA=OC,

∴AD+CO=BC+AO,
∴假设成立,
∴本项正确,
故答案为①③④.
点评:本题主要考查平行四边形的性质,利用反证法证明命题等知识点,关键在于正确的做出辅助线,熟练掌握平行四边形的性质和判定定理.

 ∴AF∥CE,∠BCA=∠DAC,
∴AF∥CE,∠BCA=∠DAC, ②假设四边形ABCD是平行四边形,
②假设四边形ABCD是平行四边形, ∴AD=BC,AB=CD,OA=OC,OB=OD,
∴AD=BC,AB=CD,OA=OC,OB=OD, ∴AD+CO=BC+AO,
∴AD+CO=BC+AO,

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案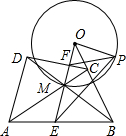 设凸四边形ABCD的对角线AC、BD的交点为M,过点M作AD的平行线分别交AB、CD于点E、F,交BC的延长线于点O,P是以O为圆心OM为半径的圆上一点(位置如图所示),求证:∠OPF=∠OEP.
设凸四边形ABCD的对角线AC、BD的交点为M,过点M作AD的平行线分别交AB、CD于点E、F,交BC的延长线于点O,P是以O为圆心OM为半径的圆上一点(位置如图所示),求证:∠OPF=∠OEP. 设凸四边形ABCD的对角线AC、BD的交点为M,过点M作AD的平行线分别交AB、CD于点E、F,交BC的延长线于点O,P是以O为圆心OM为半径的圆上一点(位置如图所示),求证:∠OPF=∠OEP.
设凸四边形ABCD的对角线AC、BD的交点为M,过点M作AD的平行线分别交AB、CD于点E、F,交BC的延长线于点O,P是以O为圆心OM为半径的圆上一点(位置如图所示),求证:∠OPF=∠OEP.