练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间，y1表示乌龟所行的路程，y2表示兔子所行的路程)．有下列说法：①“龟兔再次赛跑”的路程为1 000米；②兔子和乌龟同时从起点出发；③乌龟在途中休息了10分钟．其中正确的说法是_________________(把你认为正确说法的序号都填上)．

    【答案】①③

    【解析】

    通过认真分析函数图象就可以就可以得出龟兔赛跑的路程，各自出发的时间等，由图象的数据分析就可以得出结论．

    由函数图象，得

    “龟兔再次赛跑”的路程为1 000米，兔子子乌龟出发40分钟后出发的，乌龟在途中休息了10分钟，

    故①③正确，

    故答案为：①③．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部 ， 颖颖的头顶及亮亮的眼睛恰在一条直线上时，两人分别标定自己的位置 ， ． 然后测出两人之间的距离 ， 颖颖与楼之间的距离（ ， ， 在一条直线上），颖颖的身高 ， 亮亮蹲地观测时眼睛到地面的距离 ． 你能根据以上测量数据帮助他们求出住宅楼的高度吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形中，的平分线交于点的平分线交于点，交于点，且．

    （1）求证：四边形是平行四边形；

    （2）若，求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一块矩形木板，木工采用如图的方式，在木板上截出两个面积分别为18dm2和32dm2的正方形木板．

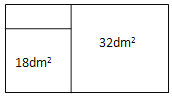
    （1）求剩余木料的面积．

    （2）如果木工想从剩余的木料中截出长为1.5dm，宽为ldm的长方形木条，最多能截出　 　块这样的木条．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．
    （1）设第x天生产空调y台，直接写出y与x之间的函数解析式，并写出自变量x的取值范围．
    （2）若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第x天的利润为W元，试求W与x之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1) 发现：

    如图1，点是线段外一动点，且，．当点位于 时，线段的长取得最大值；最大值为 (用含，的式子表示)．

    (2)应用：

    如图2，点为线段外一动点，，，分别以，为边在外部作等边和等边，连接，．

    ①求证：；

    ②直接写出线段长的最大值．

    (3)拓展：

    如图3，在平面直角坐标系中，点，点，点为线段外一动点，，，，请直接写出线段长的最大值及此时点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：有一个内角为90°，且对角线相等的四边形称为准矩形．

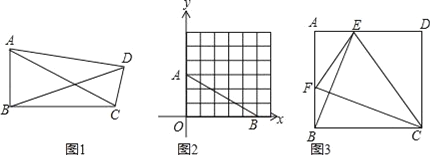
    （1）①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=　 　；

    ②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是　 　；（整点指横坐标、纵坐标都为整数的点）

    （2）如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；

    （3）已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

    （1）求证：BC是⊙O的切线；
    （2）若⊙O的半径为3，OP=1，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=。

    查看答案和解析>>

    同步练习册答案