Question

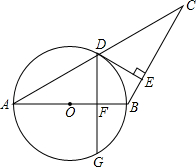
如图，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E。求证：

（1）DE是⊙O的切线；

（2）作DG⊥AB交⊙O于G，垂足为F，若∠A＝30°，AB＝8，求弦DG的长。

 

Answer 1

【答案】

（1）证明见解析；（2）.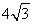

【解析】

试题分析：（1）连接OD，只要证明OD⊥DE即可．本题可根据等腰三角形中两底角相等，将相等的角进行适当的转换，即可证得OD⊥DE；
（2）求DG就是求DF的长，在直角三角形DFO中，有OD的值，∠DOF的值也容易求得，那么DG的值就求得了．

试题解析：证明：连接OD，

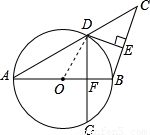
∵OA=OD，

∴∠A=∠ADO．

∵BA=BC，

∴∠A=∠C，

∴∠ADO=∠C，

∴DO∥BC．

∵DE⊥BC，

∴DO⊥DE．

∵点D在⊙O上，

∴DE是⊙O的切线．

（2）解：∵∠DOF=∠A+∠ADO=60°，

在Rt△DOF中，OD=4，

∴DF=OD•sin∠DOF=4•sin60°=．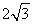

∵直径AB⊥弦DG，

∴DF=FG．

∴DG=2DF=．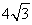

考点: 1.切线的判定；2.垂径定理；3.解直角三角形．