
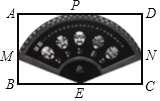
【题目】在一张矩形纸片ABCD上制作一幅扇形艺术画.扇形的圆弧和边AD相切,切点为P,BC边中点E为扇形的圆心,半径端点M,N分别在边AB,CD上,已知AB=10cm,BC=10![]() cm,则扇形艺术画的面积为_____.
cm,则扇形艺术画的面积为_____.
【答案】![]()
【解析】
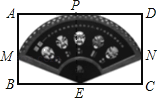
连接PE,如图,利用切线的性质得PE⊥BC,则PE=AB=10cm,再利用特殊角的三角函数值得到∠BEM=30°,∠DOG=60°,所以∠MEN=120°,然后利用扇形面积公式解答.
解:如图,连接PE.
∵扇形的圆弧和边AD相切,切点为P,E为扇形的圆心,
∴PE⊥BC.
∴四边形ABEP是矩形,
∴PE=AB=10cm.
∵BC=10![]() cm,E是BC边中点,
cm,E是BC边中点,
∴BE=5![]() cm.
cm.
在直角△BEM中,∠B=90°,BE=5![]() cm,ME=PE=10cm,
cm,ME=PE=10cm,
∴cos∠BEM=![]() .
.
∴∠BEM=30°,
∴∠MEP=60°.
同理,∠PEN=60°,
∴∠MEN=120°.
∴扇形艺术画的面积为:![]()
故答案是:![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】为迎接:“国家卫生城市”复检,某市环卫局准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费w(元)与A型垃圾箱x(个)之间的函数关系式;
②当买A型垃圾箱多少个时总费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向上的抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,函数值
,函数值![]() 的最小值是
的最小值是![]() .
.
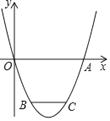
(1)求抛物线的解析式.
(2)点![]() 为抛物线上的点,并在对称轴的左侧.作
为抛物线上的点,并在对称轴的左侧.作![]() 轴交抛物线于点
轴交抛物线于点![]() ,连结
,连结![]() ,
,![]() ,且
,且![]() .
.
①求![]() 的值.
的值.
②若点![]() 在线段
在线段![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径画圆.当
为半径画圆.当![]() 和
和![]() 的一边相切时,求点
的一边相切时,求点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
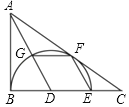
【题目】如图,在△ABC中,E为BC边上一点,以BE为直径的AR半圆D与AC相切于点F,且EF∥AD,AD交半圆D于点G.
(1)求证:AB是半圆D的切线;
(2)若EF=2,AD=5,求切线长AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推进球类运动的发展,某校组织校内球类运动会,分篮球、足球、排球、羽毛球、乒乓球五项,要求每位学生必须参加一项并且只能参加一项,某班有一名学生根据自己了解的班内情况绘制了如图所示的不完整统计表和扇形统计图.

请根据图表中提供的信息,解答下列问题:
(1)图表中m=________,n=________;
(2)若该校学生共有1000人,则该校参加羽毛球活动的人数约为________人;
(3)该班参加乒乓球活动的4位同学中,有3位男同学(分别用A,B,C表示)和1位女同学(用D表示),现准备从中选出两名同学参加双打比赛,用树状图或列表法求出恰好选出一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:

⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
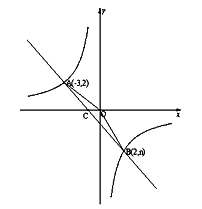
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于A(
的图像相交于A(![]() )、B(
)、B(![]() )两点。
)两点。
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)根据图像直接写出使一次函数的值大于反比例函数的值的![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com