
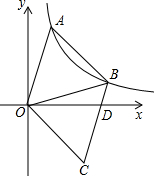
 如图,已知等边三角形OAB与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则$\frac{BD}{DC}$的值为$\frac{\sqrt{3}-1}{2}$.(已知sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$)
如图,已知等边三角形OAB与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则$\frac{BD}{DC}$的值为$\frac{\sqrt{3}-1}{2}$.(已知sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$) 分析 作辅助线,构建直角三角形,根据反比例函数的对称性可知:直线OM:y=x,求出∠BOF=15°,根据15°的正弦列式可以表示BF的长,证明△BDF∽△CDN,可得结论.
解答 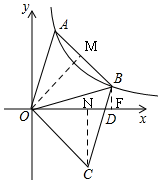 解:如图,过O作OM⊥AB于M,
解:如图,过O作OM⊥AB于M,
∵△AOB是等边三角形,
∴AM=BM,∠AOM=∠BOM=30°,
∴A、B关于直线OM对称,
∵A、B两点在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且反比例函数关于直线y=x对称,
∴直线OM的解析式为:y=x,
∴∠BOD=45°-30°=15°,
过B作BF⊥x轴于F,过C作CN⊥x轴于N,
sin∠BOD=sin15°=$\frac{BF}{OB}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
∵∠BOC=60°,∠BOD=15°,
∴∠CON=45°,
∴△CNO是等腰直角三角形,
∴CN=ON,
设CN=x,则OC=$\sqrt{2}$x,
∴OB=$\sqrt{2}$x,
∴$\frac{BF}{\sqrt{2}x}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
∴BF=$\frac{(\sqrt{3}-1)x}{2}$,
∵BF⊥x轴,CN⊥x轴,
∴BF∥CN,
∴△BDF∽△CDN,
∴$\frac{BD}{CD}=\frac{BF}{CN}$=$\frac{\frac{(\sqrt{3}-1)x}{2}}{x}$=$\frac{\sqrt{3}-1}{2}$,
故答案为:$\frac{\sqrt{3}-1}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、等边三角形的性质、等腰直角三角形的性质和判定、三角函数、三角形相似的性质和判定、翻折的性质,明确反比例函数关于直线y=x对称是关键,在数学题中常设等腰直角三角形的直角边为未知数x,根据等腰直角三角形斜边是直角边的$\sqrt{2}$倍表示斜边的长,从而解决问题.


科目:初中数学 来源: 题型:选择题
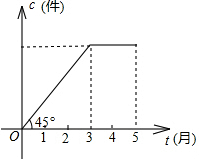 某村办工厂2016年前五个月生产某种产品的总量c(万件)与时间t(月)的函数图象如图所示,则该厂对这种产品来说( )
某村办工厂2016年前五个月生产某种产品的总量c(万件)与时间t(月)的函数图象如图所示,则该厂对这种产品来说( )| A. | 1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少 | |
| B. | 1月至3月每月生产总量逐月增加,4、5两月生产总量与3月持平 | |
| C. | 1月至3月每月生产总量不变,4、5两月均停止生产 | |
| D. | 1月至3月每月生产总量逐月增加,4、5两月均停止生产 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
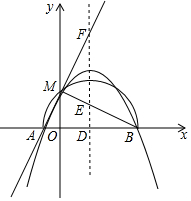 已知二次函数y=-x2+bx+c+1,
已知二次函数y=-x2+bx+c+1,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
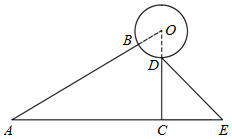 某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com