
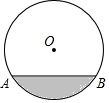
 如图,水平放置的圆形管道横截面圆半径为50cm,现在水面宽度AB为60cm,当水面宽度为80cm时,则水面比原来上涨的高度为10cm或70cm.
如图,水平放置的圆形管道横截面圆半径为50cm,现在水面宽度AB为60cm,当水面宽度为80cm时,则水面比原来上涨的高度为10cm或70cm. 分析 作OD⊥AB于D,延长OD交圆于点C,连结OB,利用垂径定理得到D为AB的中点,求出BD的长,在直角三角形BOD中,利用勾股定理求出OD,同理求出水面宽度为80cm时水面的高度,然后相减即可.
解答 解:如图,作OD⊥AB于D,延长OD交圆于点C,连结OB,
则D为AB的中点,即AD=BD=$\frac{1}{2}$AB=30cm,
在Rt△BOD中,根据勾股定理得:OD2=OB2-BD2=502-302=1600,
所以OD=40,
当水面宽度为80cm时,分两种情况:
①如果A′B′=80cm,连结OB′,设OC与A′B′交于点E,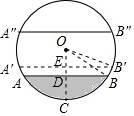 则E为A′B′的中点,即A′E=B′E=$\frac{1}{2}$A′B′=40cm,
则E为A′B′的中点,即A′E=B′E=$\frac{1}{2}$A′B′=40cm,
在Rt△B′OE中,根据勾股定理得:OE2=OB′2-B′E2=502-402=900,
所以OE=30,
则水面比原来上涨的高度为40-30=10(cm);
②如果A″B″=80cm,同理求出水面比原来上涨的高度为40+30=70(cm);
故答案为10cm或70cm.
点评 此题考查了垂径定理的应用,以及勾股定理,熟练掌握垂径定理是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
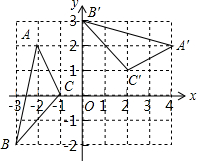 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )| A. | ( 0,1) | B. | ( 1,-1) | C. | ( 0,-1) | D. | ( 1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com