
分析 方程组$\left\{\begin{array}{l}{{y}_{1}=kx+k-1}\\{{y}_{2}=(k+1)x+k}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$,直线y1=kx+k-1与x轴的交点为($\frac{1-k}{k}$,0),y2=(k+1)x+k与x轴的交点为( $\frac{-k}{k+1}$,0),先计算出SK的面积,再依据规律求解.
解答 解:∵方程组$\left\{\begin{array}{l}{{y}_{1}=kx+k-1}\\{{y}_{2}=(k+1)x+k}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$,
∴两直线的交点是(-1,-1),
∵直线y1=kx+k-1与x轴的交点为($\frac{1-k}{k}$,0),y2=(k+1)x+k与x轴的交点为( $\frac{-k}{k+1}$,0),
∴Sk=$\frac{1}{2}$×|-1|×|$\frac{1-k}{k}$-$\frac{-k}{k+1}$|=$\frac{1}{2}$|$\frac{1}{k}$-$\frac{1}{k+1}$|,
∴S1+S2+S3+…+S2013=$\frac{1}{2}$×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$)
=$\frac{1}{2}$×(1-$\frac{1}{2014}$)
=$\frac{1}{2}$×$\frac{2013}{2014}$=$\frac{2013}{4028}$.
故答案为:$\frac{2013}{4028}$.
点评 本题考查的是一次函数图象上点的坐标特点.熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )| A. | AB∥DE且AB=DE | B. | ∠DEC=∠B | C. | AD∥EC且AD=EC | D. | BC=AD+EC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买苹果数 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
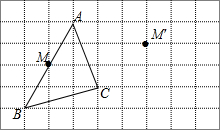 (1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.
(1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com