
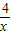 (x>0)图象上的三个整点(即横、纵坐标均为整数的点),分别以这些点向横轴或纵轴作垂线段,由垂线段为边作出三个正方形,再以正方形的边长为直径作两个半圆,组成如图所示的阴影部分,则阴影部分的面积总和是 .(用含π的代数式表示)
(x>0)图象上的三个整点(即横、纵坐标均为整数的点),分别以这些点向横轴或纵轴作垂线段,由垂线段为边作出三个正方形,再以正方形的边长为直径作两个半圆,组成如图所示的阴影部分,则阴影部分的面积总和是 .(用含π的代数式表示)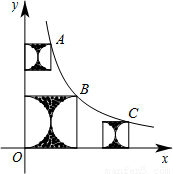
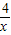 (x>0)图象上的三个整点(即横、纵坐标均为整数的点),利用整除性易得A点坐标为(1,4),B点坐标为(2,2),C点坐标为(4,1),则三个正方形的边长分别为1,2,1,而每个正方形内的阴影部分的面积都等于正方形的面积减去一个圆的面积,则根据正方形和圆的面积公式得到阴影部分的面积总和=1-π•(
(x>0)图象上的三个整点(即横、纵坐标均为整数的点),利用整除性易得A点坐标为(1,4),B点坐标为(2,2),C点坐标为(4,1),则三个正方形的边长分别为1,2,1,而每个正方形内的阴影部分的面积都等于正方形的面积减去一个圆的面积,则根据正方形和圆的面积公式得到阴影部分的面积总和=1-π•( )2+4-π•12+1-π•(
)2+4-π•12+1-π•( )2.
)2.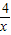 (x>0)图象上的三个整点(即横、纵坐标均为整数的点),
(x>0)图象上的三个整点(即横、纵坐标均为整数的点), )2+4-π•12+1-π•(
)2+4-π•12+1-π•( )2
)2 π.
π. π.
π.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数y=
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比列函数y=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 例如图.现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
例如图.现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:| 3 |
| 4 |
| 3 |
| 4 |
| 48 |
| x |
| 48 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com