
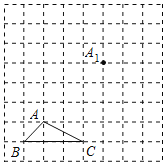
【题目】如图,正方形网格中,小正方形的边长为1.△ABC的顶点都在格点上.
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1逆时针旋转90°,在网格中画出旋转后的△A1B2C2;
(3)在(2)的条件下,直接写出点C1至点C2的经过的路径长.
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C做⊙O 的切线,与AE的延长线交于点D,且AD⊥CD.
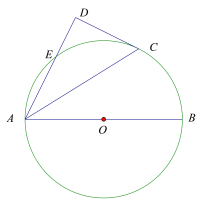
(1)求证:AC平分∠DAB;
(2)若AB=10,CD=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
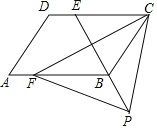
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
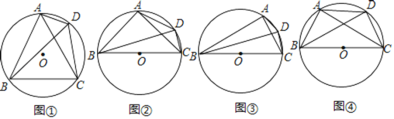
【题目】(1)方法选择:如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.
小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…
小军认为可用补短法证明:延长CD至点N,使得DN=AD…
请你选择一种方法证明.
(2)类比探究:(探究1)如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,井证明你的结论.
(探究2)如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是 .
(3)拓展猜想:如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国出租车(巡游出租车和网约出租车)客运量结构变化.
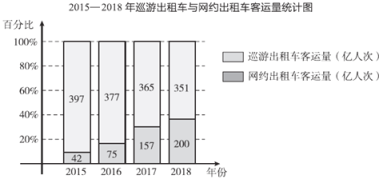
(以上数据摘自《中国共享经济发展年度报告(2019)》)
根据统计图提供的信息,下列推断合理的是( )
A.2018年与2017年相比,我国网约出租车客运量增加了20%以上
B.2018年,我国巡游出租车客运量占出租车客运总量的比例不足60%
C.2015年至2018年,我国出租车客运的总量一直未发生变化
D.2015年至2018年,我国巡游出租车客运量占出租车客运总量的比例逐年增加
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
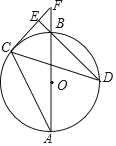
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y=x的图象与反比例函数![]() 的图象有一个交点的纵坐标是2,求:
的图象有一个交点的纵坐标是2,求:
(1)x=﹣3时反比例函数的值;
(2)当﹣3<x<﹣1时反比例函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 郑州某商场在“六一”儿童节购进一批儿童智力玩具.已知成批购进时单价20元,调查发现:该玩具的月销售量y(个)与销售单价x(元)之间满足一次函数关系,下表是月销售量、销售单价的几组对应关系:
月销售单价x/元 | 30 | 35 | 40 | 45 |
月销售量y/个 | 230 | 180 | 130 | m |
(1)求y与x的函数关系式;
(2)根据以上信息填空:
①m=______;
②当销售单价x=______元时,月销售利润最大,最大利润是______元;
(3)根据物价部门规定,每件玩具售价不能高于40元,若月销售利润不低于2520元,试求销售单价x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com