
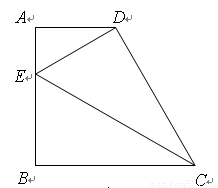
(12分)如图1,在四边形ABCD的AB边上任取一点E(点E不与点A、点B
重合),分别连接ED、EC,可以把四边形ABCD分成3个三角形.如果其中有2个三角形
相似,我们就把点E叫做四边形ABCD的AB边上的相似点;如果这3个三角形都相似,
我们就把点E叫做四边形ABCD的AB边上的强相似点.
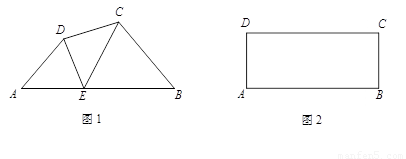
(1)若图1中,∠A=∠B=∠DEC=50°,说明点E是四边形ABCD的AB边上的相似点;
(2)①如图2,画出矩形ABCD的AB边上的一个强相似点.(要求:画图工具不限,不写画法,保留画图痕迹或有必要的说明.)
②对于任意的一个矩形,是否一定存在强相似点?如果一定存在,请说明理由;如果不一定存在,请举出反例.
(3)在梯形ABCD中,AD∥BC,AD<BC,∠B=90°,点E是梯形ABCD的AB边上的一个强相似点,判断AE与BE的数量关系并说明理由.
解:(1)理由:∵∠A=50°,
∴∠ADE+∠DEA=130°.
∵∠DEC=50°,
∴∠BEC+∠DEA=130°.
∴∠ADE=∠BEC. …………………………………………………………1分
∵∠A=∠B,
∴△ADE∽△BEC. …………………………………………………………2分
∴点E是四边形ABCD的AB边上的相似点. ……………………………3分
(2)①以CD为直径画弧,取该弧与AB的一个交点即为所求.(若不用圆规画图,则必须在图上标注直角符号或对直角另有说明.)………………………5分
②对于任意的一个矩形,不一定存在强相似点,如正方形.(答案不惟一,若学生画图说明也可.) ………………………………………………………6分
(3)第一种情况:
∠A=∠B=∠DEC=90°,∠ADE=∠BEC=∠EDC,
即△ADE∽△BEC∽△EDC.
方法一:
如图1,延长DE,交CB的延长线于点F, ………………………………7分

说明DE=EF, ………………………………………………………………8分
说明AE=BE. ………………………………………………………………9分
方法二:
如图2,过点E作EF⊥DC,垂足为F. ………………………………7分

因为∠ADE=∠CDE,∠BCE=∠DCE,
所以AE=EF,EF=BE.
所以AE=BE. ………………………………………………………………9分
方法三:
由△ADE∽△EDC可得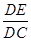 =
=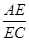 ,即AE=
,即AE=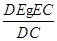 .
…………………7分
.
…………………7分
同理,由△BEC∽△EDC可得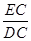 =
= ,即BE=
,即BE=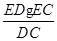 , ……………8分
, ……………8分
所以AE=BE. ………………………………………………………………9分
第二种情况:
如图3,∠A=∠B=∠EDC=90°,∠ADE=∠BCE=∠DCE,
即△ADE∽△BCE∽△DCE.
所以∠AED=∠BEC=∠DEC=60°,……………………………………10分
说明AE= DE,BE=
DE,BE= CE,DE=
CE,DE= CE,
CE,
(或说明BE=DE,AE= DE,)
DE,)
所以AE= BE.
BE.
综上,AE=BE或AE= BE.………………………………………………12分
BE.………………………………………………12分
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
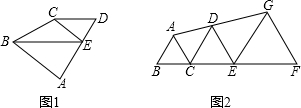
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com