
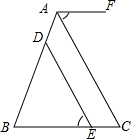
 如图,点D、E分别在AB、BC上,AF∥BC,DE∥AC.求证:∠1=∠2
如图,点D、E分别在AB、BC上,AF∥BC,DE∥AC.求证:∠1=∠2 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
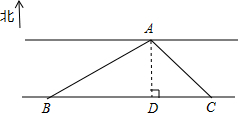 聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)
聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
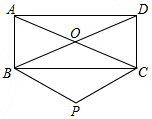 如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.
如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1800-200}{x}=\frac{1800-200}{2x}+10$ | B. | $\frac{1800+200}{x}=\frac{1800+200}{2x}+10$ | ||
| C. | $\frac{1800-200}{x}=\frac{1800-200}{2x}-10$ | D. | $\frac{1800+200}{x}=\frac{1800+200}{2x}-10$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{48}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{4a+4}$ | D. | $\sqrt{14}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com