
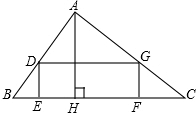
 如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.
如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y. =500米,
=500米,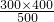 =240米;
=240米; =
=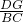 ,
, =
= ,
,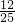 x+240,
x+240,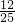 x+240)=-
x+240)=-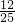 x2+240x;
x2+240x;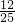 x2+240x=-
x2+240x=-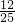 (x-250)2+3000,
(x-250)2+3000,

科目:初中数学 来源: 题型:
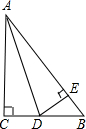 如图,有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则△DEB的面积为( )
如图,有一块直角三角形纸片,两直角边AC=30cm,BC=40cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则△DEB的面积为( )| A、250cm2 | B、150cm2 | C、200cm2 | D、100cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
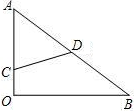 如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是
如图,有一块直角三角形的木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是查看答案和解析>>
科目:初中数学 来源: 题型:
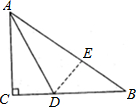 如图,有一块直角三角形纸片,其中∠C=90°,AC=6cm,BC=8,D为BC上一点,现将其沿AD折叠,使点C落在斜边AB的E处,则CD=
如图,有一块直角三角形纸片,其中∠C=90°,AC=6cm,BC=8,D为BC上一点,现将其沿AD折叠,使点C落在斜边AB的E处,则CD=查看答案和解析>>
科目:初中数学 来源: 题型:
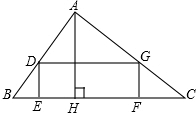 如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.
如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
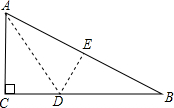 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角三角形纸片沿直线AD折叠,使点C恰好落在斜边AB上点E处.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角三角形纸片沿直线AD折叠,使点C恰好落在斜边AB上点E处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com