
【题目】如图,![]() 是正三角形
是正三角形![]() 内的一点,且
内的一点,且![]() .若将
.若将![]() 绕点
绕点![]() 逆时针旋转后,得到
逆时针旋转后,得到![]() ,则点
,则点![]() 与点
与点 ![]() 之间的距离为________
之间的距离为________![]() _____________.
_____________.

【答案】6, 150°.
【解析】
由题意根据旋转的性质分析,并利用等边三角形的判定方法得到△PAP′为等边三角形,再根据等边三角形的性质以及根据勾股定理的逆定理进行分析求解.
解:∵△PAC绕点A逆时针旋转60°后,得到△P′AB,
∴∠PAP′=60°,PA=P′A=6,P′B=PC=10,
∴△PAP′为等边三角形,
∴PP′=PA=6,∠P′PA=60°,
在△BPP′中,P′B=10,PB=8,PP′=6,
∵62+82=102,
∴PP′2+PB2=P′B2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=∠P′PB+∠BPP′=60°+90°=150°.
故答案为:6,150°.


科目:初中数学 来源: 题型:
【题目】(1)①如图1,已知![]() ,
,![]() ,可得
,可得![]() __________.
__________.

②如图2,在①的条件下,如果![]() 平分
平分![]() ,则
,则![]() __________.
__________.

③如图3,在①、②的条件下,如果![]() ,则
,则![]() __________.
__________.
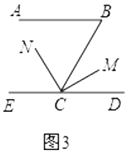
(2)尝试解决下面问题:已知如图4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
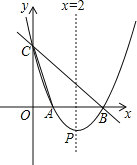
【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求该抛物线的函数表达式;
(2)请问在抛物线上是否存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)过S(0,4)的动直线l交抛物线于M,N两点,试问抛物线上是否存在定点T,使得不过定点T的任意直线l都有∠MTN=90°?若存在,请求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校长暑假将带领该校前级“三好学生”去北京大学游学,甲旅行社说:如果校长买全票一 张,则其余的学生可享受半价优惠.乙旅行社说:“包括校长在内全部按票价的六折优惠”. 若全票价为![]() 元,两家旅行社的服务质量相同,根据三好学生的人数你认为选择哪一 家旅行社才会比较合算?
元,两家旅行社的服务质量相同,根据三好学生的人数你认为选择哪一 家旅行社才会比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y=![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com