
 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示) 分析 根据等腰直角三角形的性质可得出x1=y1,x2=2x1+y2,x3=2x1+2x2+y3,…,再由点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,可得出x1•y1=x2•y2=x3•y3=…=xn•yn=1,从而得出yn=$\sqrt{n}$-$\sqrt{n-1}$,由xn•yn=1即可得出点Pn的坐标.
解答 解:∵△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,
∴x1=y1,x2=2x1+y2,x3=2x1+2x2+y3,…,
∴xn=2(x1+x2+…+xn-1)+yn.
∵点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,
∴x1•y1=x2•y2=x3•y3=…=xn•yn=1.
∴x1=y1=1,y2=$\sqrt{2}$-1,y3=$\sqrt{3}$-$\sqrt{2}$,…,yn=$\sqrt{n}$-$\sqrt{n-1}$(n是大于或等于2的正整数),
∴xn=$\frac{1}{{y}_{n}}$=$\sqrt{n}$+$\sqrt{n-1}$(n是大于或等于2的正整数).
∴点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$).
故答案为:($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$).
点评 本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质以及规律型中点的坐标,解题的关键是求出yn=$\sqrt{n}$-$\sqrt{n-1}$.本题属于中档题,难度不大,解决该题型题目时,结合反比例函数图象上点的坐标特征以及等腰直角三角形的性质,找出点Pn纵坐标的变化规律是关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
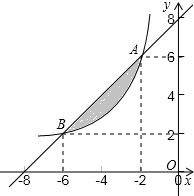 如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.
如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
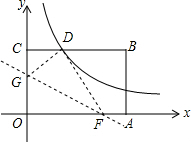 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
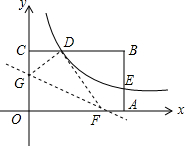 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,$\frac{2}{3}$).
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,$\frac{2}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
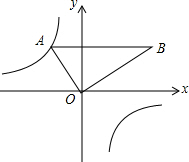 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k$>\frac{1}{3}$ | B. | k$<\frac{1}{3}$ | C. | k$≥\frac{1}{3}$ | D. | k$≤\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com