

分析 (1)首先确定A、B和顶点E的坐标,然后利用待定系数法即可求得函数的解析式;
(2)求得当y=1.5时,对应的x的值,则m的范围即可求得.
解答 解:(1)如图所示建立平面直角坐标系.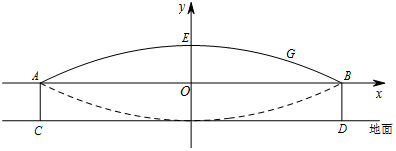
由题意可知A(-4,0),B(4,0),顶点E(0,1).
设抛物线G的表达式为y=ax2+1.
∵A(-4,0)在抛物线G上,
∴16a+1=0,解得$a=-\frac{1}{16}$.
∴$y=-\frac{1}{16}{x^2}+1$.
自变量的取值范围为-4≤x≤4.
(2)当y=1.5-1=0.5时,-$\frac{1}{16}$x2+1=0.5,
解得:x=±4$\sqrt{2}$,
∴m的取值范围是:4-4$\sqrt{2}$<m<4+4$\sqrt{2}$.
点评 本题考查了待定系数法求函数的解析式,以及二次函数的实际应用,此题为数学建模题,借助二次函数解决实际问题.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
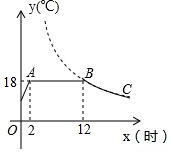 如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.
如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是反比例函数图象的一部分,则当x=20时,大棚内的温度约为10.8℃.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com