

���� ��1�����ݾ���ֵ�Լ�ż�η��ķǸ��Լ��ɵó�a��c��ֵ������b����С�����������ɵó�b��ֵ��
��2���ҳ����˶�ʱ��Ϊt��ʱ��A��B��C���ʾ������
�ٴ���t=1���ҳ�A��B��C���ʾ�������ٸ��������ľ��빫ʽ���ɵó����ۣ�
�ڴ���t=2���ҳ�A��B��C���ʾ�������ٸ��������ľ��빫ʽ���ɵó����ۣ�
�۸��������ľ��빫ʽ�ú�t�Ĵ���ʽ��ʾ��AC��AB�ij����������3AC-4AB�м��ɵó����ۣ�
��� �⣺��1����|a+2|+��c-6��2=0��b����С����������
��a=-2��b=1��c=6��
�ʴ�Ϊ��-2��1��6��
��2�����˶�ʱ��Ϊt��ʱ��A���ʾ����Ϊ-t-2��B���ʾ����Ϊ2t+1��C���ʾ����Ϊ3t+6��
�ٵ�t=1ʱ��A���ʾ����Ϊ-3��B���ʾ����Ϊ3��C���ʾ����Ϊ9��
��AC=9-��-3��=12��AB=3-��-3��=6��
�ʴ�Ϊ��12��6��
�ڵ�t=2ʱ��A���ʾ����Ϊ-4��B���ʾ����Ϊ5��C���ʾ����Ϊ12��
��AC=12-��-4��=16��AB=5-��-4��=9��
�ʴ�Ϊ��16��9��
�ۡ�AC=3t+6-��-t-2��=4t+8��AB=2t+1-��-t-2��=3t+3��
��3AC-4AB=3��4t+8��-4��3t+3��=12��
�����˶������У�3AC-4AB��ֵΪ��ֵ12��
���� ���⿼�������ᡢ�����ľ��롢�д���ʽ������ֵ�Լ�ż�η��ķǸ��ԣ�����Ĺؼ��ǣ���1�����ݶ�ֵ�Լ�ż�η��ķǸ������a��cֵ����2���ú�t�Ĵ���ʽ��ʾ��A��B��C���ʾ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 20��10 | B�� | 10��20 | C�� | 21��9 | D�� | 9��21 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | ���ӣ����ڲ��Ź�� | ||
| C�� | �����������ڽǵĺ���180�� | D�� | ���������ĺ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
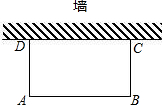 ��ͼ������һ��ǽ��ǽ�ij��Ȳ�����45m������80m�������Χһ�����γ��أ�����Χ����ʹ���γ��ص����Ϊ750m2��
��ͼ������һ��ǽ��ǽ�ij��Ȳ�����45m������80m�������Χһ�����γ��أ�����Χ����ʹ���γ��ص����Ϊ750m2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
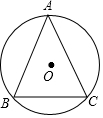 ��֪��O�İ뾶Ϊ2����ABC�ڽ��ڡ�O��$\widehat{AB}$��$\widehat{BC}$��$\widehat{AC}$�ij�֮��Ϊ3��2��3����BC�ij���
��֪��O�İ뾶Ϊ2����ABC�ڽ��ڡ�O��$\widehat{AB}$��$\widehat{BC}$��$\widehat{AC}$�ij�֮��Ϊ3��2��3����BC�ij����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com