
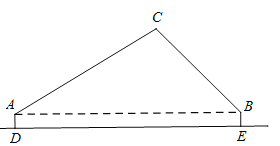
【题目】某数学小组在郊外的水平空地上对无人机进行测高实验.如图,两台测角仪分别放在A、B位置,且离地面高均为1米(即![]() 米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为
米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为![]() ,B处测得其仰角为
,B处测得其仰角为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)求该时刻无人机的离地高度;(单位:米,结果保留整数)
(2)无人机沿水平方向向左飞行2秒后到达点F(点F与点A、B、C在同一平面内),此时于A处测得无人机的仰角为![]() ,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )

A、9:4 B、3:2 C、![]() :
:![]() D、3
D、3![]() :2
:2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
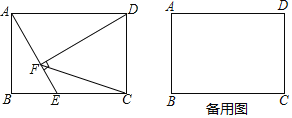
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() :
:![]() 和直线
和直线![]() :
:![]() ,点
,点![]() 和
和![]() 均在直线
均在直线![]() 上.
上.
(1)求直线![]() 的解析式;
的解析式;
(2)若抛物线过点![]() ,且抛物线与线段
,且抛物线与线段![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围;
的取值范围;
(3)将直线![]() 下移2个单位得到直线
下移2个单位得到直线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() 、
、![]() 两点,若点
两点,若点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“智慧校园”建设,某市准备为试点学校采购一批![]() 两种型号的一体机,经过市场调查发现,每套
两种型号的一体机,经过市场调查发现,每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多
型一体机的价格多![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买![]() 套
套![]() 型一体机和
型一体机和![]() 套
套![]() 型一体机.
型一体机.
(1)列二元一次方程组解决问题:求每套![]() 型和
型和![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)由于需要,决定再次采购![]() 型和
型和![]() 型一体机共
型一体机共![]() 套,此时每套
套,此时每套![]() 型体机的价格比原来上涨
型体机的价格比原来上涨![]() ,每套
,每套![]() 型一体机的价格不变.设再次采购
型一体机的价格不变.设再次采购![]() 型一体机
型一体机![]() 套,那么该市至少还需要投入多少万元?
套,那么该市至少还需要投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
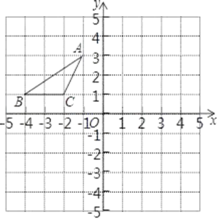
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2,点A1的对应点为点A2.
(1)画出△A1B1C1和△A2B2C2;
(2)求出在这两次变换过程中,点A经过点A1到达A2的路径总长;
(3)求线段B1C1旋转到B2C2所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
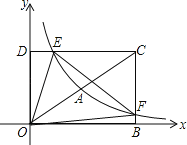
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y2=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y2=k2x+b.
(1)求反比例函数和直线EF的解析式;
(温馨提示:平面上有任意两点M(x1,y1)、N(x2,y2),它们连线的中点P的坐标为( ![]() ))(2)求△OEF的面积;
))(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x -b﹣![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,且∠MAC=∠ABC.
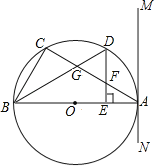
(1)求证:MN是⊙O的切线.
(2)设D是弧AC的中点,连结BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F.
①求证:FD=FG.
②若BC=3,AB=5,试求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com