B
分析:过C作AM垂直于BG,交BG于M,由已知的两组对边平行得到四边形AECG为平行四边形,可得一对同旁内角互补,再由已知的两角之比,分别求出两个角,得到∠ACG为150°,∠G为30°,在直角三角形CGM中,根据30°角所对的直角边等于斜边的一半得到CM为CG的一半,又正方形ABCD,得到三角形ABC为等腰直角三角形,O为AC的中点,根据直角三角形斜边上的中线等于斜边的一半得到OB等于AC的一半,根据平行线间的距离相等得到CM=OB,利用等量代换可得AC=CG,利用邻边相等的平行四边形为菱形可得AECG为菱形,故选项②正确;由正方形的边长,利用勾股定理求出AC的长,即为菱形的边长,可得AE的长,对选项①作出判断;由正方形ABCD得到四条边相等,四个角为直角,可得三角形ABC与三角形BCD全等,可得两三角形的面积相等,又根据平行线间的距离相等,得到三角形ABC与三角形AEC中AC边上的高相等,得到这两个三角形的面积公式,等量代换可得三角形BCD与三角形ACE的面积相等,选项③正确;根据菱形的对角线平分一组对角,得到∠CEF的度数,再由∠CFE为三角形ACF的外角,利用外角性质求出∠CFE的度数,发现∠CEF=CFE,利用等角对等边可得三角形CEF为等腰三角形,选项⑤;假设CE为

cm,在直角三角形CMG中,由斜边CG的长,利用30°角所对的直角边等于斜边的一半求出CM的长,发现直角三角形CEM中,斜边CE小于直角边CM,矛盾,故假设错误,选项④错误.
解答:过C作CM⊥EG于M,
∵BG∥AC,AE∥CG,
∴四边形AEGC为平行四边形,
∴∠ACG+∠G=180°,又∠ACG:∠G=5:1,
∴∠G=

×180°=30°,∠ACG=

×180°=150°.
在直角三角形CGM中,∠G=30°,
∴CM=

CG,
又四边形ABCD为正方形,
∴AC⊥BD,AC与BD互相平分,
在直角三角形ABC中,BO为斜边AC的中点,
∴BO=

AC,
∵AC∥BG,
∴CM=OB,
∴CG=AC,
∴四边形AEGC为菱形,选项②正确;
∵CD=AB,BC=CB,∠BCD=∠ABC=90°,
∴△BDC≌△ABC(SAS),
∴S
△BDC=S
△ABC,
又根据平行线间的距离相等,底边都为AC,
∴S
△ABC=S
△ACE,
∴S
△BDC=S
△ACE,选项③正确;
∵△ABC为等腰直角三角形,AB=BC=1cm,
∴根据勾股定理得:AC=

cm,
又四边形AECG为菱形,∴AE=AC=

cm,选项①错误;
在直角三角形CGM中,∠G=30°,
∴CM=

CG=

cm,
若CE=

cm,

<

,斜边小于直角边,矛盾,
则CE≠

cm,选项④错误;
∵四边形AECG为菱形,∠ACG=∠AEG=150°,
∴EC平分∠AEG,即∠AEC=

∠AEG=75°,
∵∠CFE为△ACF的外角,且∠CAE=∠G=30°,∠ACB=45°,
∴∠CFE=∠CAE+∠ACB=75°,
∴∠AEC=∠CFE=75°,
∴CE=CF,即△CEF为等腰三角形,选项⑤正确,
则正确的选项有②③⑤.
故答案为:②③⑤.
点评:此题考查了正方形的性质,菱形的判定与性质,等腰直角三角形的性质,全等三角形的判定与性质,等腰三角形的判定,三角形的外角性质,含30°角的直角三角形的性质,以及勾股定理,是一道综合性较强的题.

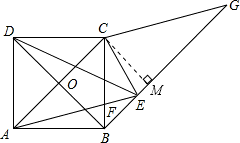
 如图,已知正方形ABCD中,对角线AC、BD交于O点,AB=1cm,过B作BG∥AC,过A作AE∥CG,且∠ACG:∠G=5:1,以下结论:①AE=
如图,已知正方形ABCD中,对角线AC、BD交于O点,AB=1cm,过B作BG∥AC,过A作AE∥CG,且∠ACG:∠G=5:1,以下结论:①AE= cm;②四边形AEGC是菱形;③S△BDC=S△AEC;④CE=
cm;②四边形AEGC是菱形;③S△BDC=S△AEC;④CE= cm;⑤△CFE为等腰三角形,其中正确的有
cm;⑤△CFE为等腰三角形,其中正确的有 cm,在直角三角形CMG中,由斜边CG的长,利用30°角所对的直角边等于斜边的一半求出CM的长,发现直角三角形CEM中,斜边CE小于直角边CM,矛盾,故假设错误,选项④错误.
cm,在直角三角形CMG中,由斜边CG的长,利用30°角所对的直角边等于斜边的一半求出CM的长,发现直角三角形CEM中,斜边CE小于直角边CM,矛盾,故假设错误,选项④错误. ∵BG∥AC,AE∥CG,
∵BG∥AC,AE∥CG, ×180°=30°,∠ACG=
×180°=30°,∠ACG= ×180°=150°.
×180°=150°. CG,
CG, AC,
AC, cm,
cm, cm,选项①错误;
cm,选项①错误; CG=
CG= cm,
cm, cm,
cm, <
< ,斜边小于直角边,矛盾,
,斜边小于直角边,矛盾, cm,选项④错误;
cm,选项④错误; ∠AEG=75°,
∠AEG=75°,

 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.