

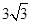 ,∠1 =30°;(2)当x=
,∠1 =30°;(2)当x=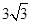 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为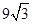 ;(3)存在, t=9或t=9﹣2
;(3)存在, t=9或t=9﹣2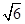 或t=12﹣
或t=12﹣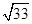 .
.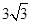 .则
.则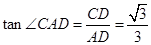 ,故∠CAD=30°;然后由平行线的性质推知∠1=∠CAD=30°;
,故∠CAD=30°;然后由平行线的性质推知∠1=∠CAD=30°;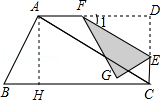
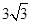
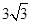 .
.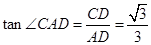
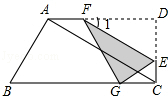
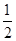 EG=
EG=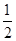 x
x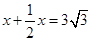
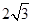 ;
;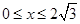 时,
时,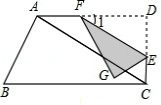
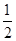 ·DE·DF=
·DE·DF=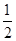 x·
x·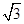 x=
x=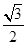 x2,
x2,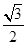 >0,对称轴为y轴
>0,对称轴为y轴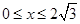 ,y随x的增大而增大
,y随x的增大而增大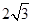 时,y最大值=
时,y最大值=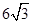 ;
;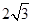 <x≤
<x≤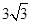 时,设FG,EG分别交BC于点M、N
时,设FG,EG分别交BC于点M、N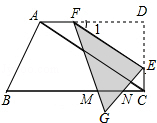
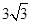 ﹣x,NE=2(
﹣x,NE=2(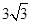 ﹣x),
﹣x),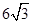 .
.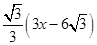 ,
,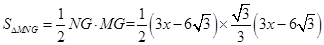
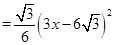 ,
,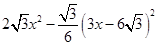 =
=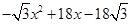 .
.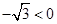 ,对称轴为直线
,对称轴为直线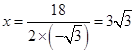 ,
,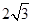 <x≤
<x≤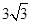 时,y有最大值,
时,y有最大值,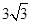 时,
时,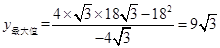 .
.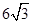 <
<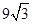
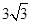 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为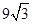 ;
;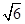
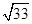 .
.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源:不详 题型:解答题
 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
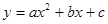 的图象如图,其对称轴x=-1,给出下列结果
的图象如图,其对称轴x=-1,给出下列结果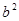 >4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是( )
>4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是( )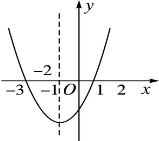
| A.①②③④ | B.②④⑤ | C.②③④ | D.①④⑤ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
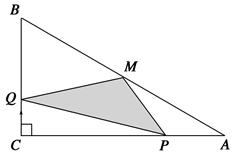
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
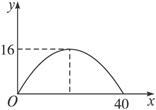
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 和
和 的关系说法中,正确的是( )
的关系说法中,正确的是( )| A.它们的形状相同,开口也相同; |
B.它们都关于 轴对称; 轴对称; |
| C.它们的顶点不相同; |
D.点( , , )既在抛物线 )既在抛物线 上也在 上也在 上 上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com