
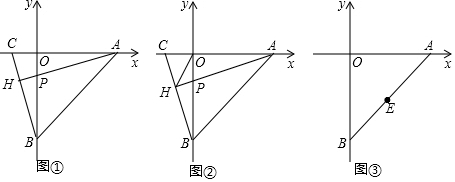
分析 (1)欲证明△AOP≌△BOC已经有一边,一角相等,只要证明∠HAC=∠OBC即可.
(2)如图②中,过O分别作OM⊥CB于M点,作ON⊥HA于N点,由△COM≌△PON(AAS),推出OM=ON.因为OM⊥CB,ON⊥HA,推出HO平分∠CHA,由此即可证明.
(3)结论:BG-BO=AF.只要证明△GOE≌△FAE,推出OG=AF,推出BG-BO=GO=AF即可证明.
解答 (1)证明:如图①中,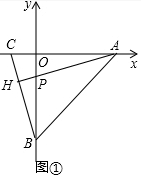
∵AH⊥BC即∠AHC=90°,∠COB=90°
∴∠HAC+∠ACH=∠OBC+∠OCB=90°,
∴∠HAC=∠OBC.
在△OAP与△OBC中,
$\left\{\begin{array}{l}{∠COB=∠POA=90°}\\{OA=OB}\\{∠OAP=∠OBC}\end{array}\right.$,
∴△OAP≌△OBC(ASA),
(2)过O分别作OM⊥CB于M点,作ON⊥HA于N点,如图②.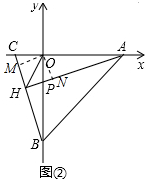
在四边形OMHN中,∠MON=360°-3×90°=90°,
∴∠COM=∠PON=90°-∠MOP.
在△COM与△PON中,
$\left\{\begin{array}{l}{∠COM=∠PON}\\{∠OMC=∠ONP=90°}\\{OC=OP}\end{array}\right.$,
∴△COM≌△PON(AAS),
∴OM=ON.
∵OM⊥CB,ON⊥HA,
∴HO平分∠CHA,
∴∠OHP=$\frac{1}{2}$∠CHA=45°,
∵∠AHB=90°,
∴2∠OHP=∠AHB.
(3)结论:BG-BO=AF.
理由如下:连接OE,如图3.
∵∠AOB=90°,OA=OB,E为AB的中点,
∴OE⊥AB,∠BOE=∠AOE=45°,OE=EA=BE,
∴∠OAD=45°,∠GOE=90°+45°=135°,
∴∠EAF=135°=∠GOE.
∵GE⊥EF即∠GEF=90°,
∴∠OEG=∠AEF,
在△GOE与△FAE中,
$\left\{\begin{array}{l}{∠OEG=∠AEF}\\{OE=AE}\\{∠GOE=∠EAF}\end{array}\right.$,
∴△GOE≌△FAE,
∴OG=AF,
∴BG-BO=GO=AF,
∴BG-BO=AF.
点评 本题考查三角形综合题、全等三角形的判定和性质、角平分线的判定定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 如图甲,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形如图乙,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图甲,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形如图乙,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
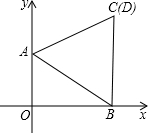 在平面直角坐标系中,已知点A(0,2),点B是x轴上一动点,以线段AB为一边,在其一边做等边三角形ABC,且点C在第一象限,当B运动到原点O处时,记此时的C点位置为点D.
在平面直角坐标系中,已知点A(0,2),点B是x轴上一动点,以线段AB为一边,在其一边做等边三角形ABC,且点C在第一象限,当B运动到原点O处时,记此时的C点位置为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x-1)2+5 | B. | y=2(x-1)2+1 | C. | y=2(x+1)2+3 | D. | y=2(x-3)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com